Crow AMSAA

The Reliability Growth platform can fit a Crow-AMSAA model, as described in MIL-HDBK-189 (1981). A Crow-AMSAA model is a nonhomogeneous Poisson process with failure intensity as a function of time t given by ρ(t) = λβtβ-1. Here, λ is a scale parameter and β is a growth parameter. This function is also called a Weibull intensity, and the process itself is also called a power law process (Rigdon and Basu 2000; Meeker and Escobar 1998). Note that the Recurrence platform fits the Power Nonhomogeneous Poisson Process. The Power Nonhomogeneous Poisson Process is equivalent to the Crow-AMSAA model, although it uses a different parameterization. See Fit Model.

The intensity function is a concept applied to repairable systems. Its value at time t is the limiting value of the probability of a failure in a small interval around t, divided by the length of this interval; the limit is taken as the interval length goes to zero. You can think of the intensity function as measuring the likelihood of the system failing at a given time. If β < 1, the system is improving over time. If β > 1, the system is deteriorating over time. If β = 1, the rate of occurrence of failures is constant.

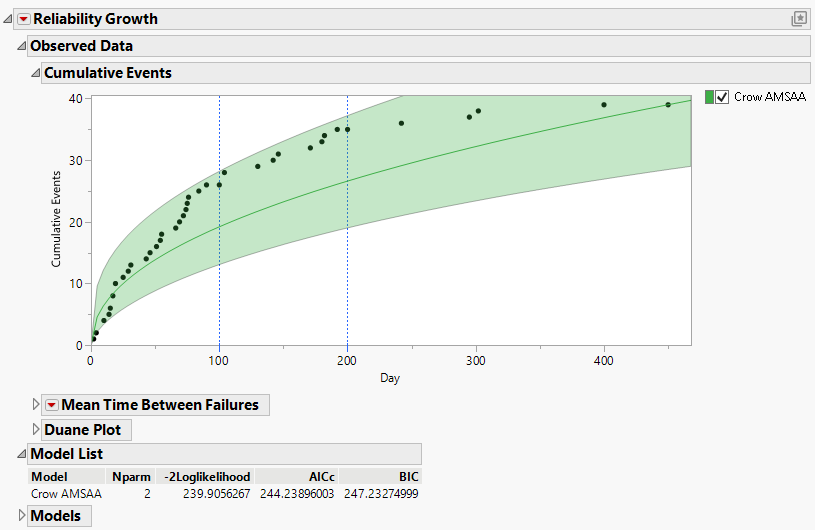
When the Crow AMSAA option is selected, the Cumulative Events plot updates to show the cumulative events curve estimated by the model. For each time point, the shaded band around this curve defines a 95% confidence interval for the true cumulative number of events at that time. The Model List report also updates. Figure 11.8 shows the Observed Data report for the data in TurbineEngineDesign1.jmp.

Figure 11.8 Crow AMSAA Cumulative Events Plot and Model List Report 

Crow-AMSAA Report

A Crow-AMSAA report opens within the Models report. If Time to Event Format is used, the Crow-AMSAA report shows an MTBF plot with both axes scaled logarithmically. See MTBF Plot.

MTBF Plot

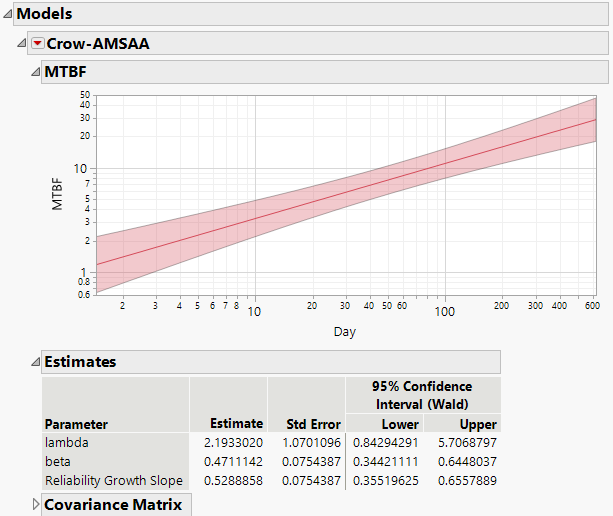
The mean time between failures (MTBF) plot is displayed by default (Figure 11.9). For each time point, the shaded band around the MTBF plot defines a 95% confidence interval for the true MTBF at time t. The plot is shown with both axes logarithmically scaled. With this scaling, the MTBF plot is linear.

Figure 11.9 MTBF Plot 

To see why the MTBF plot is linear when logarithmic scaling is used, consider the following. The mean time between failures is the reciprocal of the intensity function. For the Weibull intensity function, the MTBF is 1/(λβtβ-1), where t represents the time since testing initiation. It follows that the logarithm of the MTBF is a linear function of log(t), with slope 1 ‑ β. The estimated MTBF is defined by replacing the parameters λ and β by their estimates. So the log of the estimated MTBF is a linear function of log(t).

Estimates

Maximum likelihood estimates for lambda (λ), beta (β), and the Reliability Growth Slope (1 ‑ β), appear in the Estimates report below the plot (Figure 11.9). Standard errors and 95% confidence intervals for λ, β, and 1 ‑ β are given. For more information about the calculations, see Parameter Estimates for Crow-AMSAA Models.

Covariance Matrix

Estimated covariance matrix for the estimates of the parameters of the fitted model. This report is closed by default.

Crow-AMSAA Options

This section describes the options that are available in the Crow-AMSAA red triangle menu when a Crow AMSAA model is fit.

Show MTBF Plot

This option shows or hides the MTBF Plot. See MTBF Plot.

Show Intensity Plot

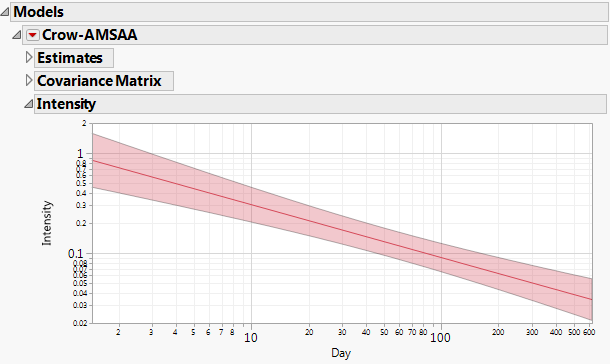
This plot shows the estimated intensity function. The Weibull intensity function is given by ρ(t) = λβtβ-1, so it follows that log(Intensity) is a linear function of log(t). Both axes are scaled logarithmically.

Figure 11.10 Intensity Plot 

Show Cumulative Events Plot

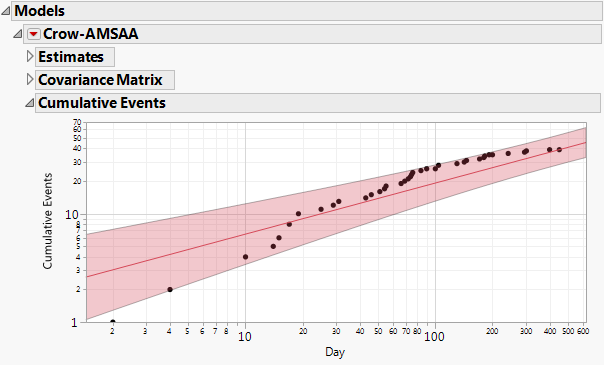
This plot shows the estimated cumulative number of events. The observed cumulative numbers of events are also displayed on this plot. Both axes are scaled logarithmically.

Figure 11.11 Cumulative Events Plot 

For the Crow-AMSAA model, the cumulative number of events at time t is given by λtβ. It follows that the logarithm of the cumulative number of events is a linear function of log(t). So, the plot of the estimated Cumulative Events is linear when plotted against logarithmically scaled axes.

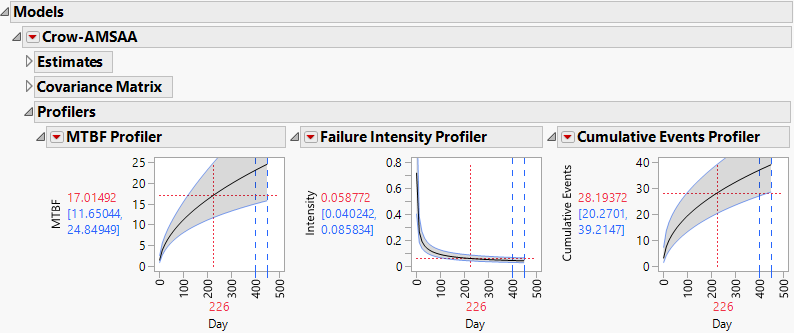
Show Profilers

Three profilers are displayed, showing estimated MTBF, Failure Intensity, and Cumulative Events. These profilers do not use logarithmic scaling. By dragging the red vertical dashed line in any profiler, you can explore model estimates at various time points; the value of the selected time point is shown in red beneath the plot. Also, you can set the time axis to a specific value by pressing Ctrl while you click in the plot. A blue vertical dashed line denotes the time point of the last observed failure.

The profilers also display 95% confidence bands for the estimated quantities. For the specified time setting, the estimated quantity (in red) and 95% confidence limits (in blue) are shown to the left of the profiler. See Profilers.

Note that you can link these profilers by selecting Factor Settings > Link Profilers from any of the profiler red triangle menus. For more information about the use and interpretation of profilers, see “Factor Profiling” in Fitting Linear Models. See also Profiler in Profilers.

Figure 11.12 Profilers 

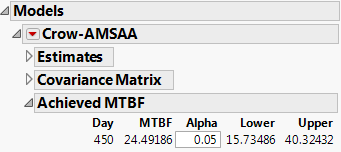
Achieved MTBF

A confidence interval for the MTBF at the point when testing concludes is often of interest. For uncensored failure time data, this report gives an estimate of the Achieved MTBF and a 95% confidence interval for the Achieved MTBF. You can specify a 100*(1-α)% confidence interval by entering a value for Alpha. The report is shown in Figure 11.13. For censored data, only the estimated MTBF at test termination is reported.

Figure 11.13 Achieved MTBF Report 

There are infinitely many possible failure-time sequences from an NHPP; the observed data represent only one of these. Suppose that the test is failure terminated at the nth failure. The confidence interval computed in the Achieved MTBF report takes into account the fact that the n failure times are random. If the test is time terminated, then the number of failures as well as their failure times are random. Because of this, the confidence interval for the Achieved MTBF differs from the confidence interval provided by the MTBF Profiler at the last observed failure time. See Crow (1982) and Lee and Lee (1978).

When the test is failure terminated, the confidence interval for the Achieved MTBF is exact. However, when the test is time terminated, an exact interval cannot be obtained. In this case, the limits are conservative in the sense that the interval contains the Achieved MTBF with probability at least 1-α.

Goodness of Fit

The Goodness of Fit report tests the null hypothesis that the data follow a Crow-AMSAA model. Depending on whether one or two time columns are entered, either a Cramér-von Mises (see Cramér-von Mises Test for Data with Uncensored Failure Times) or a chi-squared test (see Chi-Squared Goodness of Fit Test for Interval-Censored Failure Times) is performed.

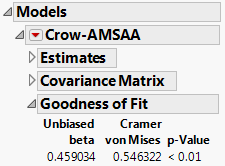
Cramér-von Mises Test for Data with Uncensored Failure Times

When the data are entered in the launch window as a single Time to Event or Timestamp column, the goodness of fit test is a Cramér-von Mises test. For the Cramér-von Mises test, large values of the test statistic lead to rejection of the null hypothesis and the conclusion that the model does not fit adequately. The test uses an unbiased estimate of beta, given in the report. The value of the test statistic is found below the Cramér-von Mises heading.

The entry below the p-Value heading indicates how unlikely it is for the test statistic to be as large as what is observed if the data come from a Crow-AMSAA model. The platform computes p-values up to 0.25. If the test statistic is smaller than the value that corresponds to a p-value of 0.25, the report indicates that its p-value is >=0.25. For more information about this test, see Crow (1975).

Figure 11.14 shows the goodness-of-fit test for the fit of a Crow-AMSAA model to the data in TurbineEngineDesign1.jmp. The computed test statistic corresponds to a p-value that is less than 0.01. The conclusion is that the Crow-AMSAA model does not provide an adequate fit to the data.

Figure 11.14 Goodness of Fit Report - Cramér-von Mises Test 

Chi-Squared Goodness of Fit Test for Interval-Censored Failure Times

When the data are entered in the launch window as two Time to Event or Timestamp columns, a chi-squared goodness of fit test is performed. The chi-squared test is based on comparing observed to expected numbers of failures in the time intervals defined. Large values of the test statistic lead to rejection of the null hypothesis and the conclusion that the model does not fit.

In the Reliability Growth platform, the chi-squared goodness of fit test is intended for interval-censored data where the time intervals specified in the data table cover the entire time period of the test. This means that the start time of an interval is the end time of the preceding interval. In particular, intervals where no failures occurred should be included in the data table. If some intervals are not consecutive, or if some intervals have identical start and end times, the algorithm makes appropriate accommodations. But the resulting test is only approximately correct.