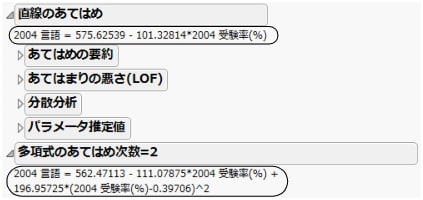
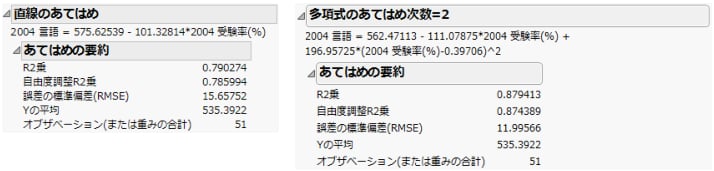
ヒント: 式はクリックして編集できます。
「直線のあてはめ」と「多項式のあてはめ 次数=X」の各レポートには、少なくとも3つのレポートが表示されます。Xがまったく同じ値になっているデータ行がある場合は、4つ目の「あてはまりの悪さ(LOF)」レポートも表示されます。
次図の「あてはめの要約」レポートは、同じデータに直線と2次多項式をあてはめたときの要約です。このレポートを比較すると、直線から2次多項式にすることで、どの程度、モデルのあてはまりが良くなるのかが分かります。「R2乗」が大きくなるほど、「誤差の標準偏差(RMSE)」の値が小さくなるほど、モデルのあてはまりは良くなっています。
Xがまったく同じ値になっているデータ行がある場合には、あてはめられたモデルが正しいかどうかに関係なく、誤差の大きさを推定できます。このような反復(Xが同じ値になっているデータ行)から計算された誤差を 純粋誤差(pure error)と言います。純粋誤差は、データの誤差のうち、どのようなモデルを構築しても説明や予測ができない変動を表します。なお、自由度が非常に少ない(反復されているXの行数が少ない)場合は、「あてはまりの悪さ(LOF)」検定はあまり役に立たない可能性があります。
モデルの残差誤差から、純粋誤差を引いたものを、あてはまりの悪さ(LOF; Lack Of Fit)の誤差といいます。指定したモデルが不適切だと、LOF誤差が純粋誤差よりも有意に大きくなります。その場合は、別のモデルをあてはめるようにしてください。「あてはまりの悪さ(LOF)」レポートには、LOF誤差が0かどうかの検定結果も表示されます。
誤差の各要因がもつ自由度(DF)。
|
–
|
「合計誤差」の自由度は、「分散分析」レポートの「誤差」の行に表示されている自由度です(第 “「分散分析」レポート”を参照)。この自由度は、データ全体の自由度から、モデルの自由度を引いたものです。「誤差」の自由度は、あてはまりの悪さ(LOF)と純粋誤差の2つの自由度に分けることができます。
|
|
–
|
「純粋誤差」の自由度は、X値が同じである行をグループにまとめ、それぞれのグループの自由度を足し合わせたものです。第 “「あてはまりの悪さ(LOF)」レポート”を参照してください。
|
|
–
|
|
–
|
|
–
|
「純粋誤差」の平方和は、X値が同じである行をグループにまとめ、それぞれのグループの平方和を足し合わせたものです。この平方和は、モデルのX効果ではまったく説明できない、純粋にランダムな誤差の大きさを推定したものです。第 “「あてはまりの悪さ(LOF)」レポート”を参照してください。
|
|
–
|
「あてはまりの悪さ(LOF)」の平方和は、「合計誤差」と「純粋誤差」の平方和の差です。LOFの平方和が大きいときは、モデルがデータに良くあてはまっていない可能性があります。この後で説明する「F値」によって、あてはまりの悪さによって生じる変動が十分に小さいかどうか、つまり、あてはまりの悪さによる変動が純粋誤差の変動に対して無視できる大きさであるかが検定されます。
|
回帰モデルに対する分散分析表では、標本全体の変動が、いくつかの成分に分割されます。これらの成分は、モデルの有効性を評価する「F値」の計算に使用されます。「F値」に関連する確率(p値)が小さいとき、「そのモデルは、Yの平均だけのモデルよりも、良くあてはまっている」と見なすことができます。
直線および多項式のあてはめの「分散分析」レポートの例は、線形式のあてはめ([直線のあてはめ])と2次式のあてはめ([多項式のあてはめ])の「分散分析」レポートです。どちらも平均だけのモデルよりも統計的にあてはまりが良いことがわかります。
|
–
|
自由度は、非欠測値の標本サイズ(N)から、使用したパラメータ数を引いて求めます。標本全体の変動においては、全体平均を表す1つのパラメータだけが使用されるので、標本サイズから自由度が1つ引かれます。例では、全体の自由度は50となっています。「全体(修正済み)」の自由度は、「モデル」項と「誤差」項に分かれます。
|
|
–
|
「直線のあてはめ」では、切片のパラメータに、傾きのパラメータを1つ追加したモデルが推定されます。分散分析表における「モデル」の自由度は、1です。また、2次の「多項式のあてはめ」では、切片のパラメータに、2つのパラメータ(
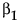 と と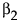 )を追加したモデルが推定されます。分散分析表における「モデル」の自由度は2となります。 )を追加したモデルが推定されます。分散分析表における「モデル」の自由度は2となります。 |
|
–
|
|
–
|
直線および多項式のあてはめの「分散分析」レポートの例の例では、各応答から標本平均までの距離の平方和(「全体(修正済み)」)は57,278.157です。これは、基本モデル(単純な平均モデル)の平方和で、その他のモデルとの比較に使用されます。
|
|
–
|
線形回帰においては、各点から直線までの距離の平方和は12,012.733に減少します。これが、線形モデルでは説明できない「誤差」(残差)の平方和です。2次多項式をあてはめると、残差の平方和は6,906.997になり、直線のときよりわずかに多く変動が説明されていることになります。言い換えると、2次多項式の方が、直線よりもモデル平方和が大きくなっており、より多くの変動を説明しています。「全体 (修正済み)」の平方和から「誤差」の平方和を引くと、モデルで説明される平方和が求められます。
|
平方和を関連する自由度で割った値。統計的検定で使用される「F値」は、次に示す2つの平均平方の比です。
|
–
|
「直線のあてはめ」の「モデル」平均平方は45,265.4です。この値は、「(切片を除く)すべての回帰パラメータが0である」という仮説のもとでは誤差分散の推定値になります。
|
|
–
|
「誤差」平均平方である245.2は、 誤差分散の推定値です。
|
モデルの平均平方を誤差の平均平方(MSE)で割ったもの。これは、「(切片を除く)すべての回帰パラメータが0である」という帰無仮説を検定します。この仮説が真のとき、「誤差」と「モデル」の平均平方は両方とも誤差分散の推定値となり、その比はF分布に従います。0でないパラメータがある場合、「F値」は通常、帰無仮説が正しいという仮定のもとで期待される値よりも大きくなります。
「直線のあてはめ」の「パラメータ推定値」レポートには、項として切片とX変数が1つ表示されています。
「各パラメータが0である」という帰無仮説を検定する統計量。t値は、パラメータ推定値とその標準誤差の比です。帰無仮説が真のとき、t値はStudentのt分布に従います。
それぞれのt値から計算した有意確率。これは、帰無仮説が真であるという仮定のもとで、計算されたt値より(絶対値が)大きいt値が得られる確率を示します。値が0.05(場合によっては0.01)より小さいときは、パラメータがゼロとは有意に異なる証拠と得られた結果は解釈されます。
追加の統計量を表示するには、レポートを右クリックし、[列]の各オプションを選択します。次の統計量はデフォルトでは表示されません。
標準β