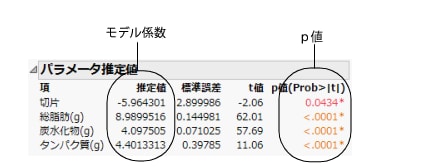
第 “1つの予測変数による回帰分析”では、予測変数1つと応答変数1つから成る単回帰モデルを紹介しました。重回帰では、複数の予測変数を用いて応答変数の平均を予測します。
この例では、キャンディバーの栄養価情報を記録した「Candy Bars.jmp」データテーブルを使用します。
|
•
|
|
•
|
|
•
|
重回帰を用いて、これら3つの予測変数から応答変数の平均を予測します。
|
1.
|
［ヘルプ］>［サンプルデータライブラリ］を選択し、「Candy Bars.jmp」を開きます。
|
|
2.
|
［グラフ］>［散布図行列］を選択します。
|
|
3.
|
「カロリー」を選択し、［Y, 列］をクリックします。
|
|
4.
|
|
5.
|
［OK］をクリックします。
|
図5.26 散布図行列の結果
引き続き、キャンディバーのサンプルデータ「Candy Bars.jmp」を使用します。
|
1.
|
［分析］>［モデルのあてはめ］を選択します。
|
|
2.
|
「カロリー」を選択し、［Y］をクリックします。
|
|
3.
|
|
4.
|
「強調点」メニューから［要因のスクリーニング］を選択します。
|
図5.27 「モデルのあてはめ」ウィンドウ
|
5.
|
［実行］をクリックします。
|
「予測値と実測値のプロット」には、カロリーの予測値と実測値が表示されます。予測値が実測値に近いほど、散布図上の点が赤い線の近くに分布します。予測値と実測値のプロットを参照してください。すべての点が赤い線の非常に近くに分布しているため、モデルはカロリーを良く予測していることがわかります。
図5.28 予測値と実測値のプロット
モデルの予測力を示す別の指標として、R2乗値（予測値と実測値のプロットの図の下部に表示されています）があります。R2乗値は、カロリーの変動のうち、モデルによって説明できる割合を表します。この値が1に近いほど、モデルの予測力は高くなります。この例では、R2乗値は0.99です。
|
•
|
図5.29 「パラメータ推定値」レポート
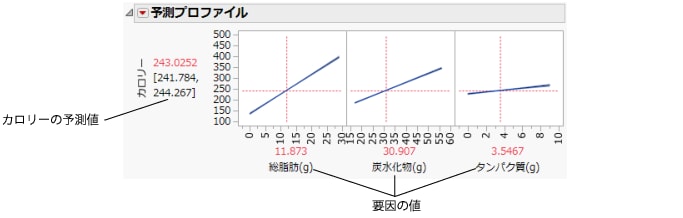
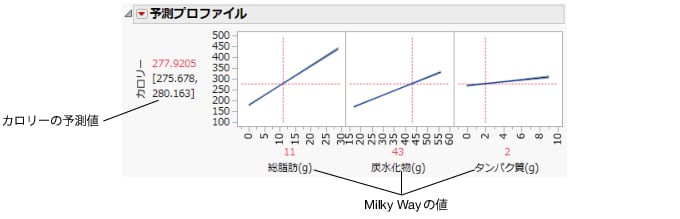
「予測プロファイル」では、要因の変化が予測値に与える影響を確認できます。プロファイルに示されている直線は、各要因の変化に伴うカロリーの変化の程度を示しています。「総脂肪(g)」の直線が一番急勾配になっています。つまり、総脂肪の変化がカロリーに一番影響を与えます。
図5.30 予測プロファイル
図5.31 Milky Wayの要因値
