1変数による平均の比較
1つの連続尺度のY変数に対して、1つのカテゴリカルなX変数がある場合、X変数の水準間で平均を比較できます。
シナリオ
この例では、会社情報のサンプルデータ「Companies.jmp」を用います。このデータには、製薬業界とコンピュータ業界における32社の財務データが記録されています。
証券アナリストは、次の点を調査する必要があります。
• コンピュータ関連企業と製薬会社において、利益は異なっているか
この比較を行うには、「利益($M)」を「タイプ」にあてはめます。
関係の洗い出し
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Companies.jmp」を開きます。
2. 「Companies.jmp」データテーブルが開いたままになっている場合は、行が除外されたり、非表示になっている可能性があります。行をデフォルトの状態(すべての行を対象に含め、いずれも非表示にしない)に戻すには、[行]>[行の属性をクリア]を選択します。
3. [分析]>[二変量の関係]を選択します。
4. 「利益($M)」を選択し、[Y, 目的変数]をクリックします。
5. 「タイプ」を選択し、[X, 説明変数]をクリックします。
6. [OK]をクリックします。
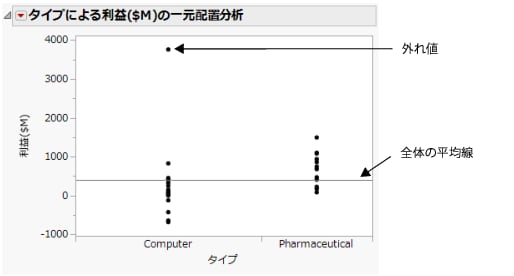
図5.15 会社のタイプ別の利益
「タイプ」が「Computer」のグループには、外れ値が1つあります。この外れ値があるせいで、散布図におけるY軸の範囲が広くなり、利益を比較しにくくなっています。この外れ値を除外し、非表示にします。
1. 外れ値をクリックします。
2. [行]>[除外する/除外しない]を選択します。該当するデータ点が計算の対象から外されます。
3. [行]>[非表示/再表示]を選択します。該当するデータ点がすべてのグラフで非表示になります。
4. 外れ値を除外してプロットを再作成するには、「タイプによる利益($M)の一元配置分析」の赤い三角ボタンをクリックし、メニューから[やり直し]>[分析のやり直し]を選択します。元の散布図ウィンドウは閉じてもかまいません。
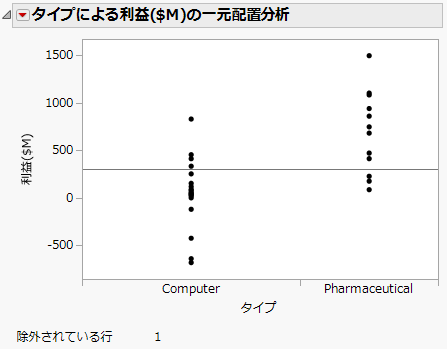
図5.16 更新後の図
外れ値を削除した結果、データがより把握しやすくなりました。
5. 関係の分析を続けるには、「タイプによる利益($M)の一元配置分析」の赤い三角ボタンをクリックし、メニューから次のオプションを選択します。
– [表示オプション]>[平均線]。散布図に平均線が追加されます。
– [平均と標準偏差]。平均と標準偏差を示すレポートが表示されます。
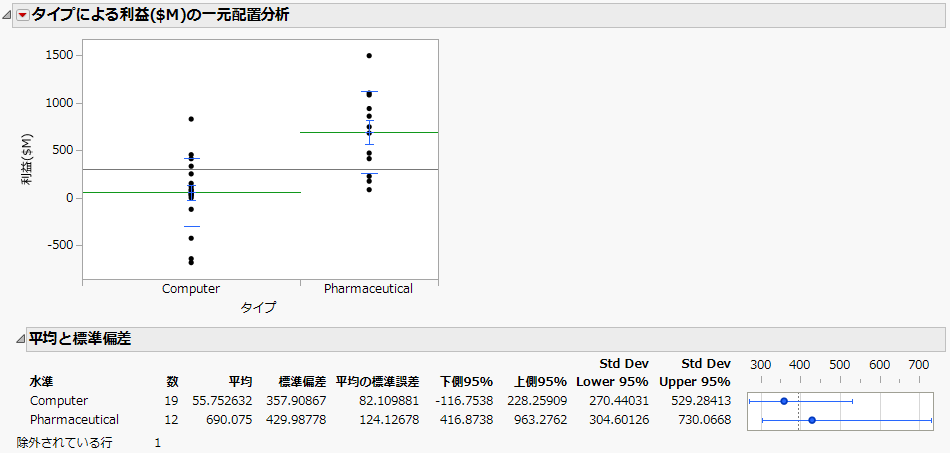
図5.17 平均線とレポート
結果の解釈
証券アナリストは、コンピュータ関連企業と製薬会社の利益を比較する必要がありました。更新後の散布図から、製薬会社の方がコンピュータ関連企業よりも平均利益が高いことがわかります。レポートに示されている2つの平均値の差を計算すると、利益の差は約6億3,500万ドルになります。散布図からは、コンピュータ関連企業の中には赤字の会社があるのに対し、製薬会社は全社とも黒字であることも判明します。
t検定の実行
ここまでは、限られた標本(データテーブル内の会社)に基づいて考察してきました。ここで、次の点を検討するとします。
• 母集団において差はあるのか、それとも6億3,500万ドルの差は偶然だけで起きたものなのか
• 差がある場合には、それはどれぐらいなのか
これらの回答を導き出すには、二標本t検定を実行します。t検定の結果は、標本データをもとに、母集団について推論したものになっています。
t検定を実行するには、「一元配置分析」の赤い三角ボタンをクリックし、メニューから[平均/ANOVA/プーリングしたt検定]を選択します。
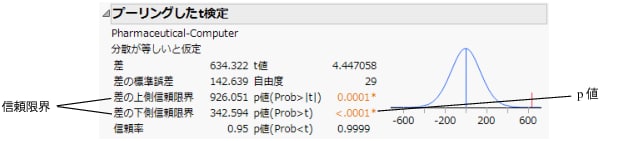
図5.18 t検定の結果
p値0.0001は有意水準0.05よりも小さいので、統計的に有意です。したがって、標本データの平均利益の差は偶然だけの産物ではないと結論付けることができます。つまり、製薬会社の平均利益とコンピュータ関連企業の平均利益は、母集団においても異なると言えます。
結論の導き出し
信頼限界の値によって、2業種の平均利益にどの程度の差があるかを判断します。Figure 5.18の「差の上限信頼限界」と「差の下限信頼限界」の値を見てください。これらの結果から、製薬会社の平均利益はコンピュータ関連企業の平均利益よりも3億4,300万ドルから9億2,600万ドル高いという結論が導き出されます。