効果の詳細
「最小2乗法によるあてはめ」レポートの「効果の詳細」オプションは、各効果に関するグラフや検定などを表示します。「モデルのあてはめ」起動ウィンドウで選択した強調点に基づき、レポートの内容は変わります。
• 強調点で[効果てこ比]オプションを選択した場合は、各効果に関するレポートが、ウィンドウの上部、「モデル全体」レポートの右側に表示されます。このとき、「てこ比プロット」も描かれます。
• 強調点で[要因のスクリーニング]または[最小レポート]を選択した場合、「効果の詳細」レポートが含まれますが、最初は閉じています。レポートを表示するには、開閉アイコンをクリックしてください。
「効果の詳細」レポートの先頭は、最小2乗平均表です。ただし、連続尺度の効果に関しては、この表は表示されません。赤い三角ボタンのメニューから特定のオプションを選択することにより、最小2乗平均に対する検定を行うことができます。
効果のオプションの表
効果名の赤い三角ボタンのメニューには、次のようなオプションが含まれます。モデルの手法によっては、これらのオプションの一部は使えず、表示されない場合があります。
最小2乗平均表
効果に対する検定を行うときに比較される統計量です。最小2乗平均表を参照してください。
このオプションは、連続尺度の効果には使用できません。
最小2乗平均プロット
名義/順序尺度の主効果/交互作用に対して、最小2乗平均をプロットします。効果が交互作用の場合、このオプションを選択すると、最初に「最小2乗平均プロットのオプション」ウィンドウを呼び出されます。最小2乗平均プロットを参照してください。
最小2乗平均の対比
「対比の指定」パネルが開き、ここで、名義/順序尺度の主効果/交互作用に対して、水準を比較するための対比を指定および検定できます。最小2乗平均の対比を参照してください。
最小2乗平均のStudentのt検定
Studentのt検定を使って、最小2乗平均のペアごとの比較に関する検定と信頼区間を計算します。Studentのt検定とTukeyのHSD検定を参照してください。
メモ: この検定のp値や信頼区間は、すべての比較に対してではなく、個々の1つ1つの比較に対して計算されたものです。一般的に、すべての比較における第1種の誤りの確率は、個々の比較における第1種の誤りの確率よりも大きくなります。
最小2乗平均のTukeyのHSD検定
Tukey-KramerのHSD(Honestly Significant Difference)検定(Tukey 1953, Kramer, 1956)を使って、最小2乗平均のペアごとの比較に関する検定および信頼区間を計算します。Studentのt検定とTukeyのHSD検定を参照してください。
メモ: この検定のp値や信頼区間は、すべてのペアの比較をまとめて考慮して調整されたものです。この検定は、標本サイズが等しい場合は正確で、標本サイズが異なる場合は保守的になります(Hayter, 1984)。
最小2乗平均のDunnettの検定
指定したコントロール水準(対照群)との比較に関する検定および信頼区間を計算します。また、検定結果をグラフにします。最小2乗平均のDunnettの検定を参照してください。
輪切り検定(単純主効果検定)
交互作用内にある特定の因子の水準ごとに、別の因子に関して「全水準で平均が等しい」という帰無仮説を検定します。輪切り検定(単純主効果検定)を参照してください。
メモ: このオプションは、名義尺度および順序尺度の効果に関する交互作用にのみ使用できます。
検出力の分析
各効果の検定に対する検出力について、「検出力の詳細」レポートを表示します。検出力分析を参照してください。
最小2乗平均表
最小2乗平均は、指定のモデルで他の効果を中立的な値に固定したときの、名義/順序尺度である効果の各水準における予測値です。連続尺度の説明変数では、標本平均が「中立的な値」として使用されます。名義尺度の効果では、その効果の係数を平均した値(つまり、ゼロ)が「中立的な値」として使用されます。順序尺度の効果では、最初の水準が「中立的な値」として使われます。
最小2乗平均は、調整済み平均または調整平均と呼ばれることもあります。モデルに複数の効果がある場合、最小2乗平均は単なる平均とは違う値になります。実際の場面では、最小2乗平均の値は、標本平均よりも互いに近くなるのが普通です。これは、最小2乗平均が「中立的な値」に基づいた予測値であるためです。
最小2乗平均は他の効果を特定の値に固定したときの予測値なので、それらを比較し、検定することができます。JMPでの各効果に対する検定は、最小2乗平均に対する検定になっています。最小2乗平均の詳細については、名義尺度の因子における最小2乗平均および順序尺度の因子における最小2乗平均を参照してください。
なお、結果において、主効果に対しては、最小2乗平均と一緒に標本平均(単純な平均)も表示されます(Figure 3.10)。
最小2乗平均表の例
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Big Class.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「体重(ポンド)」を選択し、[Y]をクリックします。
4. 「年齢」、「性別」、「身長(インチ)」を選択して、[追加]をクリックします。
5. 「強調点」のリストから[要因のスクリーニング]を選択します。
6. [実行]をクリックします。
7. 「最小2乗法によるあてはめ」レポートの下のほうに「効果の詳細」レポートが表示されますが、これは最初は閉じた状態です。「効果の詳細」レポートのタイトルの横にある開閉ボタンをクリックし、レポートを開きます。
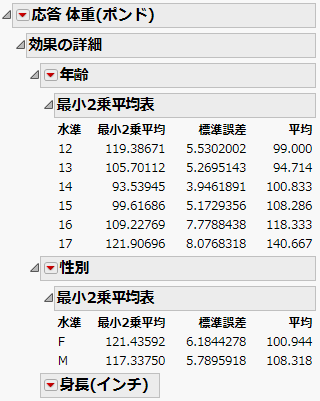
「効果の詳細」レポートには、3つの効果それぞれのレポートが表示されます(Figure 3.10)。「年齢」と「性別」には最小2乗平均表が表示されていますが、連続尺度の効果である「身長(インチ)」には表示されていません。最小2乗平均が標本平均とどのように異なるかに注目してください。
図3.10 最小2乗平均表
「最小2乗平均表」レポートには、次のような列があります。
水準
名義/順序尺度である因子の水準または水準の組み合わせ。
最小2乗平均
各水準における最小2乗平均の推定値。
推定
(最小2乗平均が推定可能でない場合にのみ表示。)最小2乗平均が推定可能でない場合の警告。
標準誤差
各水準における最小2乗平均の標準誤差。
下側95%
最小2乗平均の両側95%信頼区間の下限。[回帰レポート]>[信頼区間をすべて表示]オプションを選択した場合、またはレポートを右クリックし、[列]>[下側95%]を選択した場合にのみ表示されます。
上側95%
最小2乗平均の両側95%信頼区間の上限。[回帰レポート]>[信頼区間をすべて表示]オプションを選択した場合、またはレポートを右クリックし、[列]>[上側95%]を選択した場合にのみ表示されます。
平均
指定した水準における標本平均。バランスがとれているデータ(釣合いがとれているデータ)の場合は、最小2乗平均と同じ値になります。
最小2乗平均プロット
[最小2乗平均プロット]のオプションでは、名義/順序尺度の主効果/交互作用に対して、[最小2乗平均プロット]を作成します。効果が交互作用の場合、このオプションを選択すると、最初に「最小2乗平均プロットのオプション」ウィンドウを呼び出されます。最小2乗平均プロットのオプションを参照してください。
「最小2乗平均プロット」の赤い三角ボタンのメニューには、次のようなオプションがあります。
信頼限界の表示
プロットに描かれている各推定値に対して、その信頼区間を表示/非表示にします。
接続線の表示
プロットに表示されている各水準の最小2乗平均をつなぐ線分を表示/非表示にします。
削除
指定された効果の「最小2乗平均プロット」レポートを削除します。
最小2乗平均プロットのオプション
交互作用の赤い三角メニューから[最小2乗平均プロット]オプションを選択すると、「最小2乗平均プロットのオプション」ウィンドウが表示されます。
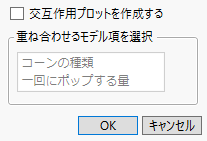
図3.11 「最小2乗平均プロットのオプション」ウィンドウ
ウィンドウで何も選択せずに[OK]をクリックすると、最小2乗平均プロットが1つ表示されます。プロットの水平軸は、複数の因子の水準を組み合わせたもので構成されています。交互作用プロットを作成するには、[交互作用プロットを作成する]の横のチェックボックスを選択します。[重ね合わせるモデル項を選択]オプションで、交互作用プロットに重ね合わせて点としてプロットする因子を選択できます。
交互作用項は3次である場合、[交互作用プロットを作成する]をオンにして重ね合わせる因子を指定すると、2番目のパネルも表示されます。2番目のパネルで何も選択せずに[OK]をクリックすると、交互作用プロットが1つだけ作成されます。2番目のパネルで、[別プロットとするモデル項を選択]で因子を選択すると、そこで選択した因子の水準ごとに個別の交互作用プロットが作成されます。
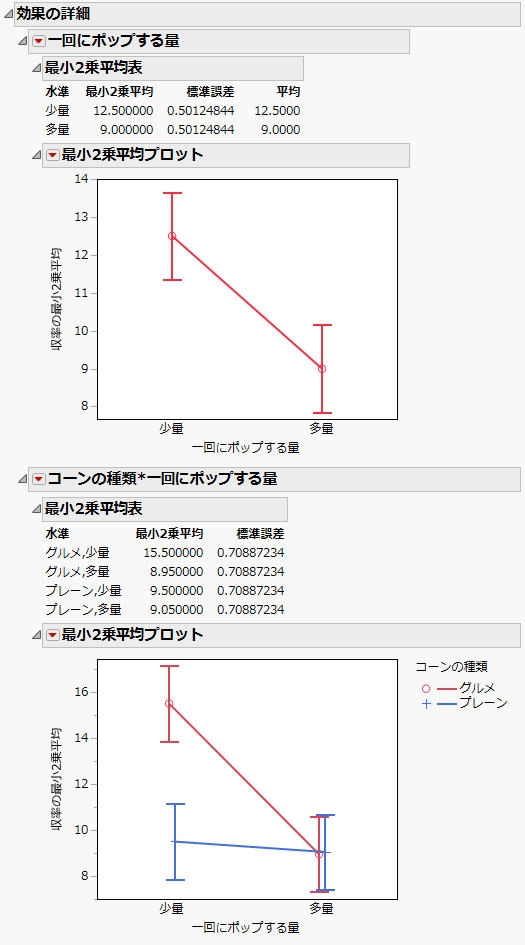
図3.12 2因子間交互作用の最小2乗平均表およびプロット
最小2乗平均プロットの例
Figure 3.12のレポートを作成するには、次の手順に従います。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Popcorn.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「収率」を選択し、[Y]をクリックします。
4. 「コーンの種類」、「油の量」、「一回にポップする量」を選択し、[マクロ]>[完全実施要因]を選択します。「強調点」が[要因のスクリーニング]に変わります。
5. [実行]をクリックします。
6. 「効果の詳細」の開閉アイコンをクリックして、7つのモデル効果の詳細を開きます。
7. 「一回にポップする量」の赤い三角ボタンをクリックして、[最小2乗平均プロット]を選択します。
8. 「コーンの種類*一回にポップする量」の赤い三角ボタンをクリックして、[最小2乗平均プロット]を選択します。「最小2乗平均プロットのオプション」ウィンドウが表示されます。
9. 「最小2乗平均プロットのオプション」ウィンドウで、[交互作用プロットを作成する]の横のチェックボックスをクリックします。
10. [重ね合わせるモデル項を選択]から、[コーンの種類]を選択します。
11. [OK]をクリックします。
12. 「コーンの種類*一回にポップする量」でプロットされている因子を入れ替えるために、step 8とstep 9を繰り返します。
13. [重ね合わせるモデル項を選択]で、[一回にポップする量]を選択して[OK]をクリックします。
図3.13 因子を入れ替えた最小2乗平均プロット
Figure 3.13は、プロットする因子を入れ替えた後の「コーンの種類*一回にポップする量」のプロットです。Figure 3.12のプロットと比較してください。これらのプロットは同じ情報を示していますが、プロットする因子を入れ替えています。
最小2乗平均の対比
対比はパラメータ値の線形結合です。「対比の指定」パネルで、複数の対比を指定し、それらがすべてゼロかどうかを検定できます(Figure 3.14)。
JMPでは、最小2乗平均に対する対比を指定できます。対比の各列は、通常、合計が0、絶対値の合計が2になるように正規化されます。対比に共変量が含まれている場合は、対比を検定するときの共変量の値を指定できます。
「対比の指定」パネルに、効果名と効果の水準名が表示されています。対比の値は、最初は0に設定されています。対比を指定するために、横にはプラス記号とマイナス記号のボタンがあります。これらのボタンをクリックして対比の値を設定します。
プラスボタンまたはマイナスボタンをクリックするたびに、合計が0、絶対値の合計が2になるように可能な限り正規化されます。線形結合を追加したい場合は、[列の新規作成]ボタンをクリックします。新しい列が表示され、ここで新しい対比を定義できます。完了したら、[完了]クリックします。「対比」レポートが表示されます(Figure 3.15)。全体の検定は、対比のすべての列に対する同時F検定です。
メモ: 指定できる最大数以上の対比の列を追加しようとした場合、対比の列は追加されず、その時点で検定が実行されます。
「対比」レポートには、同時F検定に関する次のような詳細が表示されます。
平方和
同時検定の平方和。
分子自由度
分子の自由度。
分母自由度
分母の自由度。
F値
対比の平均平方を、誤差の平均平方で割った値。
p値(Prob > F)
有意性検定のp値。
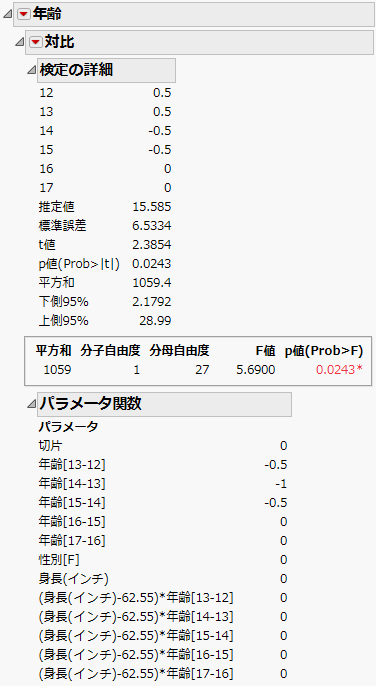
「検定の詳細」レポート
「検定の詳細」レポート(Figure 3.15)には、対比の各列に関する結果も計算されます。推定値、標準誤差、t値、p値、平方和、および、対比の推定値の信頼区間が、対比の列ごとに計算されます。
「パラメータ関数」レポート
「パラメータ関数」レポート(Figure 3.15)には、指定した対比に対応した、モデルのパラメータに関する線形結合が表示されます。
最小2乗平均の対比の例
[最小2乗平均の対比]オプションを理解するために、年齢の最初の2水準を最後の2水準と比較する方法を見ていきましょう。
次の手順に従い、Figure 3.14のようなレポートを作成します。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Big Class.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「体重(ポンド)」を選択し、[Y]をクリックします。
4. 「年齢」、「性別」、「身長(インチ)」を選択して、[追加]をクリックします。
5. 「列の選択」リストから「年齢」を選択し、「モデル効果の構成」リストから「身長(インチ)」を選択して、[交差]をクリックします。
6. [実行]をクリックします。
「最小2乗法によるあてはめ」レポートが表示されます。
7. 「年齢」の赤い三角ボタンをクリックして、[最小2乗平均の対比...]を選択します。
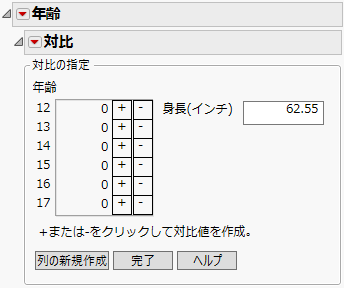
図3.14 「年齢」の対比を指定する
8. 12と13のプラス記号をクリックします。
9. 14と15のマイナス記号をクリックします。
この対比は、身長が62.55インチでの予測値に基づいて、体重の平均が2つの年齢グループ間で異なるかどうかを検定します。
10. 連続尺度の効果「身長(インチ)」の横にテキストボックスがあります。このデフォルト値は、該当する連続尺度の列の標本平均です。
11. [完了]をクリックします。
12. 「検定の詳細」レポートと「パラメータ関数」レポートを開きます。
Figure 3.15のような「対比」レポートが表示されます。対比の検定は、有意水準5%で統計的に有意です。身長が62.55インチである生徒においては、12歳と13歳の年齢グループの平均体重は、14歳と15歳の年齢グループの平均体重と、統計的に有意に異なると言えます。
図3.15 最小2乗平均の「対比」レポート
Studentのt検定とTukeyのHSD検定
Studentのt検定と、TukeyのHSD(honestly significant difference)検定のオプションは、最小2乗平均をペアごとに比較します。
• [最小2乗平均のStudentのt検定]オプションは、通常のt分布に基づき、検定結果が算出されています。各ペアに対する検定は、1つ1つの比較の有意水準に基づいています。複数の検定を行うと、全体において第1種の誤りを犯す確率は、1つあたりの検定の有意水準を上回ってしまいます。
• [最小2乗平均のTukeyのHSD検定]オプションは、Tukey検定を実行します。この検定は、先ほどのStudentのt検定とは異なり、複数の検定を行った場合の全体に対する有意水準を制御しています。このように多重性を考慮しているため、Tukey検定の信頼区間のほうが、t検定の信頼区間よりも広くなります。この検定は、標本サイズが等しい場合は正確で、標本サイズが異なる場合は保守的になります(Hayter, 1984)。
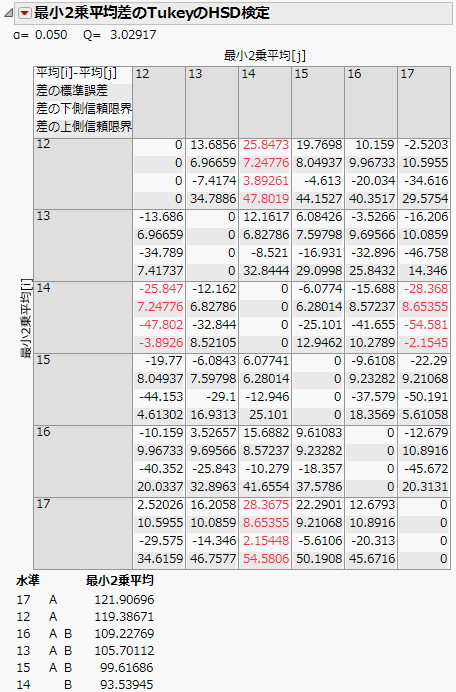
Figure 3.16は、「Big Class.jmp」サンプルデータの「年齢」に対する「最小2 乗平均差のTukeyのHSD検定」レポートです(このレポートを表示するには、このサンプルデータの「モデルのあてはめ」スクリプトを実行した後、「年齢」の赤い三角ボタンをクリックし、「最小2乗平均のTukeyのHSD検定」を選択します)。デフォルトで[クロス集計レポート]と[文字の接続レポート]が表示されます。
図3.16 「最小2乗平均のTukeyのHSD検定」レポート
クロス集計レポート
これらのオプションを選択すると、最小2乗平均の差、差の標準誤差、差の信頼限界を含むクロス集計レポートが表示されます。信頼区間や検定の有意水準と棄却値は、行列の上に表示されます。デフォルトの有意水準は0.05ですが、「モデルのあてはめ」起動ウィンドウで任意の有意水準を指定できます。平均のペアに統計的に有意な差がある場合は、該当するセルが赤色で表示されます。
文字の接続レポート
文字の接続レポートは、デフォルトでクロス集計レポートの下に表示されます。同じ文字で接続された水準、つまり同じ文字を含む水準には、統計的に有意な差がありません。共通の文字で接続されていない水準には、統計的に有意な差があります。
Figure 3.16では、水準17、12、16、13、15が文字「A」でつながっています。この接続は、5%で有意ではないことを示しています。また、水準16、13、15、14は文字「B」でつながっており、これも5%で有意ではないことを示しています。しかし、年齢17と14、年齢12と14は、同じ文字でつながっていません。これは、これら2つの水準のペアでは、統計的に有意な差があることを示しています。
ヒント: 文字の接続レポートの内側を右クリックし、[列]を選択すると、接続文字([文字])、標準誤差([標準誤差])、信頼限界([下側95%]、[上側95%])を含む列を追加することができます。「文字」列は、接続文字を1列に連結したものです。有意水準と信頼水準は、「モデルのあてはめ」起動ウィンドウの[有意水準の設定]で指定した有意水準によって決まります。
Studentのt検定とTukeyのHSD検定のオプション
各効果にある赤い三角ボタンのオプションを使用すると、表やレポートの表示と非表示を切り替えることができます。[最小2乗平均のStudentのt検定]では、次のオプションすべてが使用できます。[最小2乗平均のTukeyのHSD検定]では、最初の4つのオプションが使用できます。[クロス集計レポート]と[文字の接続レポート]は、デフォルトで表示されます。
クロス集計レポート
最小2平均の差、差の標準誤差、差の信頼限界を、水準のペアごとに示した2元表を表示します。統計的に有意な差は、赤色の字で表示されます。
文字の接続レポート
有意な差と、有意ではない差を、アルファベット文字をつなげることで示したレポートです。同じ文字でつながっていない水準は、有意差があります。同じ文字でつながっている水準は、有意ではありません。
文字の接続レポートをテーブルに保存
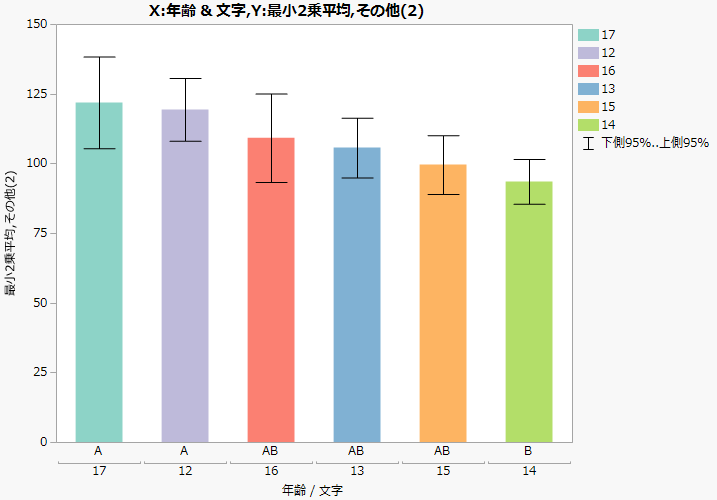
データテーブルを作成し、効果の水準、接続文字、最小2乗平均、標準誤差、信頼区間の列を保存します。このテーブルには、「棒」というスクリプトも保存されます。このスクリプトは、最小2乗平均を棒グラフとして描き、それに信頼区間のバーを重ねたグラフを作成します。棒グラフにおいて、水準は最小2乗平均の降順に並べられます。
Figure 3.17は、「Big Class.jmp」をデータとして用いた棒グラフの例です。このサンプルデータに添付されている「モデルのあてはめ」スクリプトを実行した後、「年齢」の赤い三角ボタンをクリックし、「最小2乗平均のTukeyのHSD検定」を選択してください。そして、「最小2乗平均差のTukeyのHSD検定」レポートで[文字の接続レポートをテーブルに保存]を選択します。最後に、作成されたデータテーブルで[棒]のスクリプトを実行します。
差の順位レポート
差、標準誤差、信頼区間、およびp値を差の降順に並べて表示します。また、差を棒グラフで示し、信頼区間を重ねて表示します。
詳細な比較
比較ごとに、詳細なレポートを表示します。このレポートには、差の推定値、標準誤差、信頼区間、t値、自由度、および、片側検定/両側検定のp値が表示されます。また、検定結果を視覚化した、t分布の密度曲線も表示されます。この密度曲線の影がついた領域は、両側検定のp値を表します。
図3.17 「最小2乗平均差のTukeyのHSD検定」の文字の接続レポートから作成された棒グラフ
最小2乗平均のDunnettの検定
Dunnettの検定(Dunnett, 1955)は、各群の平均を、コントロール群(対照群)の平均と比較します。Dunnettの検定では、行われる複数の比較全体に対して、第1種の誤りが制御されています。[最小2乗平均のDunnettの検定]オプションを選択すると、Dunnettの検定が行われます。一般的な状況でのp値と信頼区間の計算には、Hsuの因子分析型近似法が使用されています(Hsu, 1992)。
[最小2乗平均のDunnettの検定]を選択すると、コントロール群を指定するためのダイアログが表示されます。「最小2乗平均差のDunnettの検定」レポートには、有意水準、検定統計量の値(Q)、およびコントロール群が表示されます。
Figure 3.18は、「Cholesterol.jmp」サンプルデータの「処置群」に対して[最小2乗平均のDunnettの検定]オプションを選択したときのレポートです。この例では、応答変数を「6月午後」としています。また、コントロール群は、「処置群」列の「コントロール」です。
図3.18 「最小2乗平均差のDunnettの検定」レポート
このレポートには次の2つのオプションがあります。
コントロール群との差のレポート
このレポートは、デフォルトで表示されます。効果の各水準に対して、コントロール群と比較した水準、差の推定値、標準誤差、信頼区間、p値といった情報が表示されます。
コントロール群との差のグラフ
コントロール以外の各水準について、コントロール群との差が点で示されます。また、上側と下側の決定限界(UDL; Upper Decision Limit、LDL; Lower Decision Limit)が線で描かれます。このグラフには、[要約レポートの表示]オプションと[表示オプション]オプションがあります。[要約レポートの表示]オプションを選択すると、グラフに関する詳細情報が表示されます。[表示オプション]では、グラフの外観を変更できます。
輪切り検定(単純主効果検定)
[輪切り検定]オプションは、名義尺度や順序尺度の列から成る交互作用効果に対して使用できます。このオプションは、ある因子の水準内において、別の因子の水準がすべて等しいかどうかをF検定します。言い換えると、交互作用を「輪切り」して検定します。
たとえば、A*B*Cという交互作用を輪切り検定(単純主効果検定)するとします。ここで、因子Aの水準の1つが「小」だとします。「A =小」における輪切り検定は、「A = 小」のときの、B*C水準の最小2乗平均に差があるかどうかのF検定です。輪切り検定により、交互作用内のどこに差があるかを調べることができます。
「輪切り検定」レポートは、最小2乗平均の「対比」レポートと同じ形式になっています。最小2乗平均の対比を参照してください。
検出力分析
[検出力の分析]コマンドを選択すると、「検出力の詳細」レポートが開きます。ここで、該当する効果のF検定について、事前や事後の検出力分析を行えます。
メモ: 差を検出するのに必要な標本サイズを、実験や調査を行う前に算出する作業は、「検出力の事前計算」などと呼ばれています。実験計画は「実験計画(DOE)」プラットフォームで行えますが、検出力の事前計算には[実験計画(DOE)]>[標本サイズ/検出力]および[実験計画(DOE)]>[計画の評価]が役に立ちます。「モデルのあてはめ」を利用した検出力の事前計算の例については、検出力の事前計算を参照してください。
Figure 3.19は、「Big Class.jmp」サンプルデータの「検出力の詳細」レポートです。この「検出力の詳細」レポートで、アルファ(a; 有意水準)、シグマ(s; 誤差の標準偏差)、デルタ(d; 効果の大きさ)、数(n; 標本サイズ)を入力すると、それらの値に対する検出力が求められます。値を1つだけ(開始値のみ)入力するか、値を2つ(開始値と終了値)入力するか、もしくは、等差数列(開始値、終了値、間隔)で入力してください。入力した値に対して、検出力が計算されます。
図3.19 「検出力の詳細」ウィンドウ
検出力分析の統計的詳細を参照してください。
「検出力の詳細」ウィンドウには、次のような列とオプションが含まれます。
アルファ(a)
検定の有意水準です。この値は0~1の間で、通常は、0.05、0.01、または0.10です。「モデルのあてはめ」起動ウィンドウで[有意水準の設定]を選択して異なる値を設定していない限り、1行目にあらかじめ入力されているαの値は0.05です。
シグマ(s)
誤差の標準偏差。現在のデータとモデルから計算されたRMSE(誤差の標準偏差の推定値)が、参考値として1行目にあらかじめ入力されています。
デルタ(d)
対象となる効果の大きさ(effect size; 効果量)。効果の大きさを参照してください。1行目にあらかじめ入力されている値は、仮説の平方和を標本サイズの平方根で割った値の平方根、つまり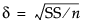 です。
です。
数(n)
標本サイズ。1行目にあらかじめ入力されている値は、現在のデータの標本サイズです。
検出力を求める
a、s、d、nから、検出力が求められます。検出力とは、指定したsおよびnのとき、有意水準aで検定が有意となり、大きさdの差が検出される確率です。検出力の計算を参照してください。
最小有意数を求める
指定したdおよびsのとき、有意水準aで検定が有意となるために必要な標本サイズの最小数を求めます。LSNの計算を参照してください。
最小有意値を求める
p値がaとなるパラメータまたはパラメータの線形関数の最小絶対値を求めます。最小有意値は、a、s、nの関数です。このオプションは、自由度が1の検定に対してだけ使用できます。LSVの計算を参照してください。
調整済み検出力と信頼区間
検出力を事後的に計算するときは、誤差分散とパラメータに関して、真値ではなく、推定値を使用します。これらの推定値を用いると、F分布の非心度パラメータの推定においてバイアスが生じます。調整済み検出力は、非心度の推定値における正のバイアスを除去するために、計算を調整して検出力を求めたものです(Wright and O’Brien 1988)。
また、調整済み検出力の信頼区間は、非心度推定値の信頼区間から算出されています。
調整済み検出力は、現在のデータから算出された推定値に基づくため、検出力やその信頼区間は、dに対する現在の推定値に対してのみ計算されます。調整済み検出力の計算を参照してください。