モデルに誤差因子が含まれる例
この例では、誤差因子からの変動を考慮した場合と考慮しない場合の最適化を比較します。このデータテーブルは、タイヤメーカーがシリカ・シラン・硫黄の含有量を因子とし、タイヤの硬度を目標値の70.0に合わせることを目的に行った実験の結果です。シランと硫黄の量は簡単(かつ精確)に制御が可能ですが、シリカは簡単には制御できず、従って誤差因子であると見なすことにしましょう。
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Tiretread.jmp」を開きます。
2. [グラフ]>[プロファイル]を選択して予測プロファイルを起動します。
3. 「予測式 硬度」に[Y, 予測式]の役割を割り当てます。
4. [OK]をクリックします。
5. 「予測プロファイル」の赤い三角ボタンをクリックし、[最適化と満足度]>[満足度関数]を選択します。
6. 「予測プロファイル」の赤い三角ボタンをクリックし、[最適化と満足度]>[満足度の設定]を選択すると、「応答目標」ウィンドウが開きます。
ヒント: 「応答目標」ウィンドウは、満足度関数のプロットをダブルクリックして開くこともできます。
7. リストから[目標値に合わせる]を選択して、[OK]をクリックします。
8. 「予測プロファイル」の赤い三角ボタンをクリックし、[最適化と満足度]>[満足度の最大化]を選択して「硬度」を目標値に一致させるような因子設定を見つけます。
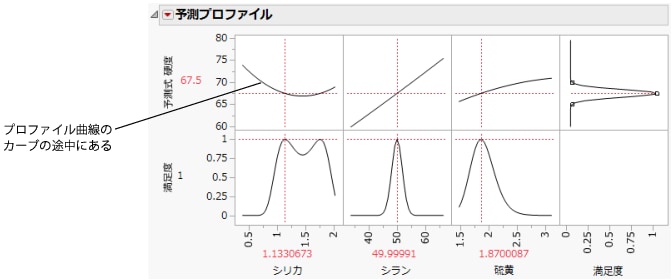
予測プロファイルは次の図のようになります。「シリカ」の最適値がプロファイル曲線のカーブの途中にあることに注意してください。これは、「シリカ」の設定のばらつきが、応答の「硬度」に影響することを示しています。
メモ: 目標値を達成する因子設定の組み合わせは1つとは限らないので、ユーザによる分析の結果がここで紹介するものと一致しないこともあります。
図3.21 「硬度」の満足度の最大化
そこで今度は、「硬度」を目標値に合わせるだけでなく、「シリカ」の設定のばらつきに影響されない設定を見つけることにします。「シリカ」を誤差因子として、再度最適化を行います。
1. [グラフ]>[プロファイル]を選択します。
2. 「予測式 硬度」を選択し、[Y, 予測式]をクリックします。
3. 「シリカ」を選択し、[誤差因子]をクリックします。
4. [OK]をクリックします。
5. 「予測プロファイル」の赤い三角ボタンをクリックし、[最適化と満足度]>[満足度関数]を選択します。
6. 「予測式 硬度」応答の満足度のプロットをダブルクリックすると、「応答目標」ウィンドウが開きます。
7. リストから[目標値に合わせる]を選択して、[OK]をクリックします。
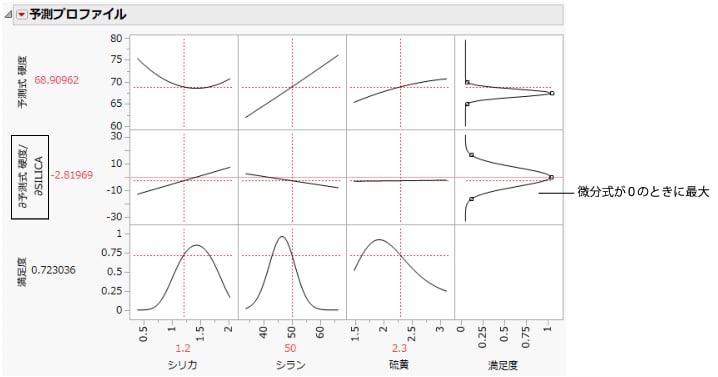
今回のプロファイルで最適化すると、目標値に近づけるだけではなくて、予測式を誤差因子で微分した式がゼロである、つまり、誤差因子において最も平坦である位置が探し出されます。
図3.22 シリカについての予測式の微分
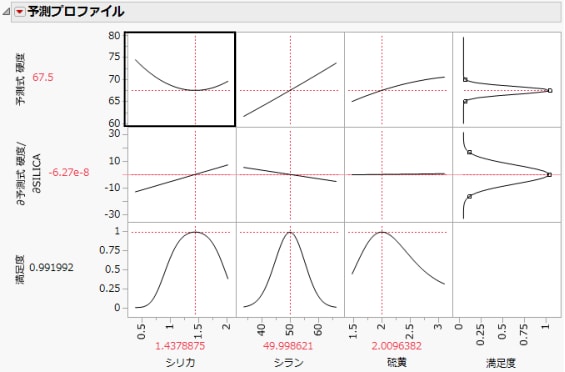
8. 「予測プロファイル」の赤い三角ボタンをクリックし、[最適化と満足度]>[満足度の最大化]を選択すると、誤差因子を考慮した上で、因子の最適設定が探し出されます。
今度は、「硬度」が目標値に一致するだけでなく、「シリカ」において平坦な領域が探し出されています。この性質により、「シリカ」曲線の傾きが大きい領域と比べて、「シリカ」のばらつきがあまり「硬度」に伝達されません。
図3.23 満足度の最大化
「シリカ」のばらつきが予測のばらつきにどれくらい影響を与えるか、簡単に確認することができます。それには、各プロファイル(誤差因子のあるものと、ないもの)で次の手順を行います。
1. 誤差因子のないプロファイルで、「予測プロファイル」の赤い三角ボタンをクリックし、[シミュレータ]を選択します。
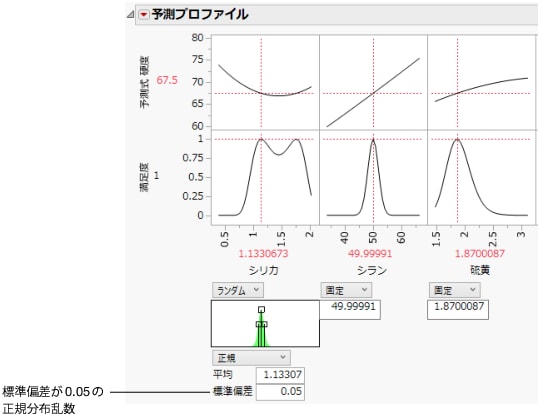
2. 「シリカ」に[ランダム]を選択し、標準偏差が0.05の正規分布の乱数を割り当てます。平均にはデフォルトを使用します。
図3.24 正規乱数の設定
3. [シミュレーション]をクリックします。
4. 「シミュレーションのデータテーブル」のグレーの三角ボタンをクリックしてから、[テーブルの作成]をクリックします。
5. 「予測式 硬度」列の名前を「誤差因子なし」に変更します。
6. 誤差因子のあるプロファイルで、「予測プロファイル」の赤い三角ボタンをクリックし、[シミュレータ]を選択します。
7. 「シリカ」に[ランダム]を選択し、標準偏差が0.05の正規分布の乱数を割り当てます。平均にはデフォルトを使用します。
8. [シミュレーション]をクリックします。
9. 「シミュレーションのデータテーブル」のグレーの三角ボタンをクリックしてから、[テーブルの作成]をクリックします。
誤差因子を考慮しなかった場合と、考慮した場合でこれらの手順を実行すると、各シミュレーションについて1つずつ、合計2つの類似したデータテーブルが得られます。2つのシミュレーションの結果として得られた予測された硬度の分布を比較します。比較を簡単にするために、2つの予測列を1つのデータテーブルに配置します。
1. 現在のシミュレーションテーブルで「予測式 硬度」列を選択して、[編集]>[最大精度でコピー]を選択します。
2. もう1つの現在のシミュレーションテーブルで、[列]>[列の新規作成]を選択します。
3. 「列名」の横に「誤差因子あり」と入力して、[OK]をクリックします。
4. 「誤差因子あり」列を選択して、[編集]>[貼り付け]を選択します。
5. [分析]>[一変量の分布]を選択します。
6. 「誤差因子あり」と「誤差因子なし」を選択して、[Y, 列]をクリックします。
7. [OK]をクリックします。
8. 「一変量の分布」の赤い三角ボタンをクリックし、[スケールの統一]を選択します。
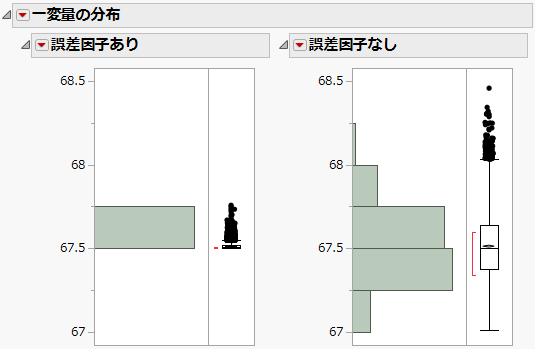
図3.25 誤差因子を考慮しなかった場合と考慮した場合の比較
ヒストグラムを見ると、分析に誤差因子を含めない場合の方が、予測された「硬度」のばらつきがずっと大きいことがわかります。
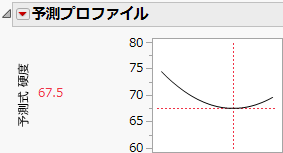
また、誤差因子を含めた場合のヒストグラムは、興味深い形状になっています。上のヒストグラムの比較を見ると、「誤差因子あり」の分布では、データが一方向だけに延びています。「一変量の分布」の赤い三角ボタンのメニューから「スケールの統一」をオフにした場合、「誤差因子あり」の分布が歪んでいることがはっきりわかります。予測が歪んでいるのは、「硬度」は「シリカ」との関係において最小となるためです(Figure 3.26)。そのため、「シリカ」にばらつきがあれば、「硬度」は増加する一方です。ロバストでない解を使用した場合、ばらつきはどちらの方向にも伝達されます。
図3.26 「シリカ」に対する「硬度」の最小値を示した予測プロファイル