応答曲面モデルの例
「モデルのあてはめ」プラットフォームの[標準最小2乗]手法を使って、応答曲面モデルをあてはめます。ここでの分析目的は、応答を最小化するような因子設定を探し出すことです。
完全な応答曲面モデルをあてはめる
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Design Experiment」フォルダにある
「Custom RSM.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
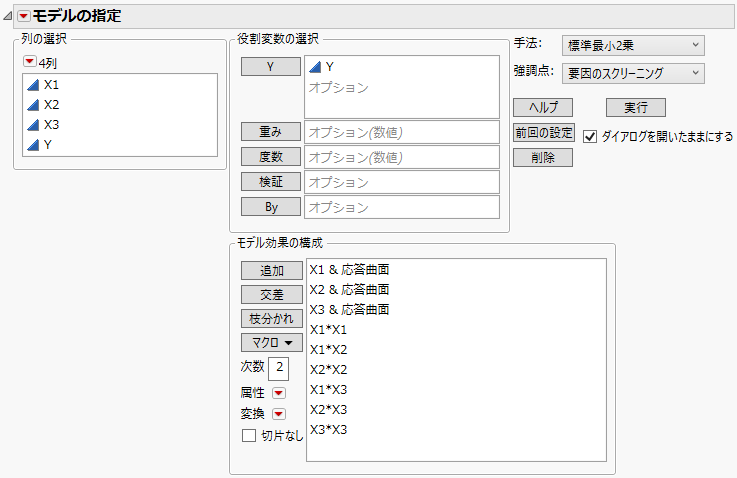
データテーブルに「モデル」スクリプトがあるため、「モデルの指定」ウィンドウは、スクリプトの指定どおりに入力された状態で開きます。次のことを注意してください。
– 「モデル効果の構成」リストを見ると、主効果の後ろに「&応答曲面」という属性がついていて、[応答曲面]のマクロが適用されていることがわかります。
– X1、X2、X3の3つの説明変数から構成される、すべての応答曲面の効果がモデルに含まれています。
– モデルの項に「&応答曲面」がついているため、分析結果に「応答曲面」レポートも出力されます。
図4.9 応答曲面分析の「モデルのあてはめ」起動ウィンドウ
3. [実行]をクリックします。
効果のさらなる削除
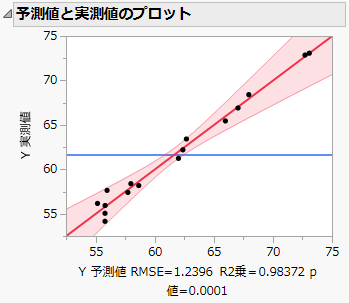
「予測値と実測値のプロット」を見ると、モデルが有意なことがわかります。あてはまりの悪さを示す証拠はありません。
図4.10 完全モデルの「予測値と実測値のプロット」
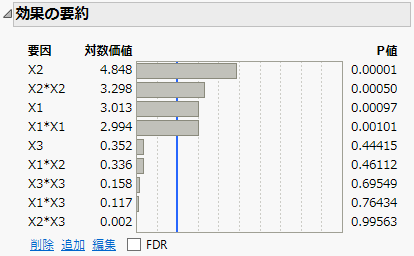
「効果の要約」レポートを見ると、多くの効果が有意でないことがわかります。特に「X2*X3」は、p値が0.99563で有意度が最も低い効果となっています。次に「効果の要約」レポートを使い、モデルから効果を対話式に削除していってみましょう。
図4.11 「効果の要約」レポート
1. 「効果の要約」レポートで「X2*X3」をクリックし、[削除]をクリックします。
モデルが更新されます。
「効果の要約」レポートのp値の列を見ると、「X1*X3」が有意でないことがわかります。
2. 「X1*X3」をクリックし、[削除]をクリックします。
「X3*X3」のp値を見ると、この効果が有意でないことがわかります。
3. 「X3*X3」をクリックし、[削除]をクリックします。
4. 「X1*X2」をクリックし、[削除]をクリックします。
「X3」が有効でないことがわかります。この効果は高次の効果に含まれていないので、削除しても親子関係(階層関係)の原則に違反しません。効果の親子関係を参照してください。
5. 「X3」をクリックし、[削除]をクリックします。
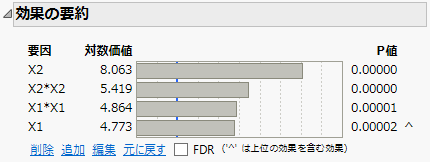
図4.12 モデル縮小後の「効果の要約」レポート
残った効果は、すべて有意です。
「応答曲面」レポートを検討する
1. 「応答 Y」の赤い三角ボタンをクリックし、[推定値]>[予測式の表示]を選択します。
図4.13 予測式
ヒント: 「予測式」は、予測の計算に使用する式です。この計算式は、[列の保存]>[予測式]を選択して表示することもできます。
以下の手順では、予測式を表示してモデル係数を確認します。
2. まず「応答曲面」レポート、次に「正準曲率」レポートを開きます。
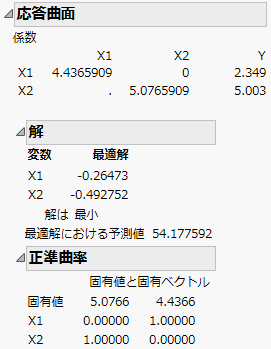
図4.14 「応答曲面」レポート
最初の表には、2次の項に対するモデル係数が行列の形式で表されています。「X1*X1」の係数は4.4365909、「X2*X2」の係数は5.0765909、「X1*X2」の係数は0です。1次項に対する係数は、「Y」という列に表示されており、「X1」で2.349、「X2」で5.003です。
「解」レポートには、最適解が表示されています。2次の応答曲面は、臨界点において、最大となっているか、最小となっているか、または、鞍点となっているか、のいずれかの状態になっています。この例の「解」レポートを見ると、応答曲面は臨界点において最小値となっており、54.18に達します。そのときの因子設定は、X1 = -0.265、X2 = -0.493です。
「正準曲率」レポートは、2次の項に対するモデル係数の行列を、固有値分解した結果です。固有値分解の結果から、曲面の形状と、主軸の方向を知ることができます。「正準曲率」レポートを参照してください。
この例ではどちらの固有値も正なので、曲面は最小値をもちます。最大固有値(5.0766)に対応した固有ベクトルの方向が、曲面が最も大きくカーブしている方向です。方向は、対応する固有ベクトル成分によって定義されます。最初の方向は「X2」の方向です(第1固有ベクトルにおいて、X2の要素が1.00となっています)。2番目の方向は、「X1」の方向です(第2固有ベクトルにおいて、X2の要素が1.00となっています)。
予測プロファイルを使って臨界点を見つける
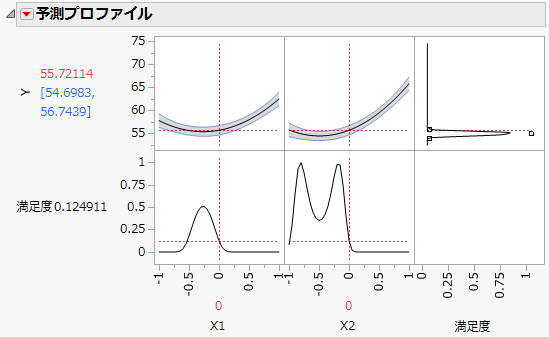
「予測プロファイル」レポートを見ると、「X1」と「X2」においては軌跡がすり鉢状になっているのがわかります。「応答変数の限界」列プロパティが「Y」に設定されているため、プロファイルには満足度関数も表示されます。
図4.15 目標値に合わせることを目的とした予測プロファイル
「応答変数の限界」列プロパティでは、目標が[目標値に合わせる]に設定されています。この例では、「Y」を目標値に合わせるのではなく、最小化することが目的です。したがって、設定を次のように変更します。
1. Ctrlキーを押しながら予測プロファイルの右上のセルをクリックします。
2. 「応答目標」ウィンドウで、オプションのリストから[最小化]を選択します。
3. [OK]をクリックします。
満足度関数に、「Y」を最小化するという目標が反映されます。
4. 「予測プロファイル」の赤い三角ボタンをクリックし、[最適化と満足度]>[満足度の最大化]を選択します。
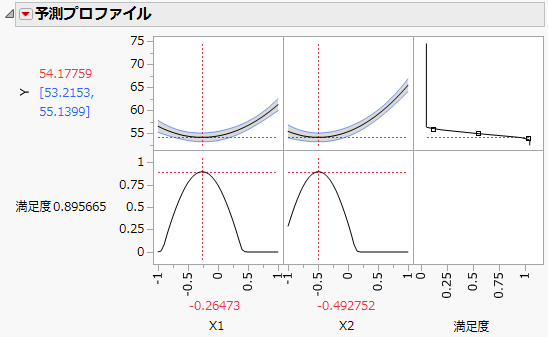
図4.16 最小化を目的とした予測プロファイルと最大化された満足度
計画の範囲内で「Y」を最小化する設定が、プロファイルの下に表示されます。設定は、「解」レポートに表示されている最適解と一致します。
「等高線プロファイル」を使って曲面を確認する
「等高線プロファイル」は、応答曲面の等高線を示します。最適解付近での応答の予測値を、別の形で表示したプロファイルです。
1. 「応答 Y」の赤い三角ボタンをクリックし、[因子プロファイル]>[等高線プロファイル]を選択します。
2. 「等高線プロファイル」の赤い三角ボタンをクリックし、[等高線グリッド]を選択します。
3. 「増分」として「1」を入力します。
4. [OK]をクリックします。
1単位間隔の等高線が描画されます。Figure 4.17を参照してください。
5. 「予測プロファイル」の赤い三角ボタンをクリックし、[因子設定]>[すべてのプロファイルを連動]を選択します。
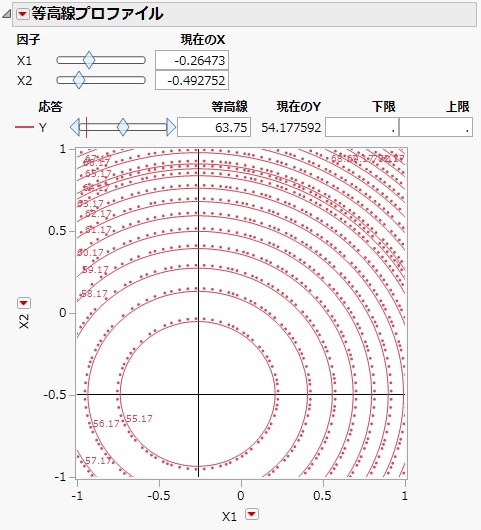
図4.17 「等高線プロファイル」で十字ツールを最適解に置いたところ
「等高線プロファイル」と「予測プロファイル」を連動させると、「等高線プロファイル」の「現在のX」の値が「予測プロファイル」の「X」の値と連動します。「予測プロファイル」の「X」の値は、「Y」が最小であるときに最適解となります。「等高線プロファイル」の十字ツールは、最適解を示しています。「現在のY」は54.177592で、「予測プロファイル」に従って予測された最小値と一致しています。
工程因子を、応答を最適化する値ちょうどには設定できないことがよくあります。「等高線プロファイル」を使えば、そのような場合でも実現できる工程因子の設定値を特定できます。次の手順では、工程の「X1」と「X2」の値を小数点以下1桁までの精度でしか設定できず、設定値は、小数点以下1桁の範囲で上下どちらにも変動し得ると想定しましょう。
6. 「等高線プロファイル」レポートの「現在のX」で、「X1」の行に「-0.3」、「X2」の行に「-0.5」を入力します。
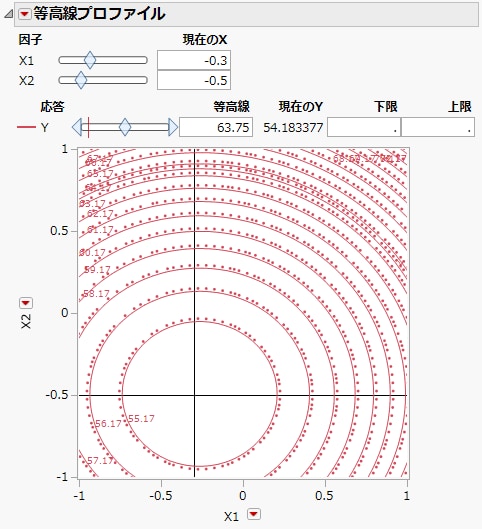
図4.18 X1 = -0.3、X2 = -0.5の値を示した「等高線プロファイル」
十字ツールは、最も内側の等高線のさらに内側にあり、「現在のY」(「現在のX」におけるYの予測値)は54.183377と、予測された最小値である54.177592とはわずかに異なります。
7. 「等高線プロファイル」で十字ツールをクリックしてドラッグし、X1 = -0.3、X2 = -0.5の点から0.1単位の半径内で「現在のX」の値を調べてみましょう。
Yの予測値は、いずれも54.4を下回ります。最も内側の等高線は55.17ですので、その等高線内のどの点に移動してもYの予測値が55.17よりも大きくなることはありません。