バギングを使用して予測精度を高める例
この例では、予測プロファイルによるバギングを使用します。4つの応答変数を3つの因子の関数として同時にモデル化するニューラルネットワークモデルの予測値を向上させることが目標です。バギングが使用されるさまざまな理由の中に、予測精度の向上があります。また、特に不安定なモデルで役立ちます。
ニューラルネットワークモデルのあてはめ
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Tiretread.jmp」を開きます。
2. [分析]>[予測モデル]>[ニューラル]を選択します。
3. 「摩擦」・「引張応力」・「伸び」・「硬度」を選択し、[Y, 目的変数]をクリックします。
4. 「シリカ」・「シラン」・「硫黄」を選択し、[X, 説明変数]をクリックします。
5. [OK]をクリックします。
6. (オプション)「乱数シード値」に「2121」と入力します。
メモ: ニューラルネットワークモデルでは、検証セットが無作為に抽出されるため、結果がいつも同じではありません。上記のものと同じ乱数シード値を入力すると、以下の結果を再現できます。
7. [実行]をクリックします。
8. 「モデル NTanH(3)」の赤い三角ボタンをクリックし、[計算式の保存]を選択します。
メモ: このオプションを使用すると、ニューラルネットワークモデルのすべての応答変数の予測値がデータテーブルに保存されます。後で、これらの値をバギングから得た予測値と比較します。
バギングの実行
初期モデルを作成したら、このモデルを使ってバギングを実行します。バギングは、[予測プロファイル]から実行できます。
1. 「モデル NTanH(3)」の赤い三角ボタンをクリックし、[プロファイル]を選択します。
レポートの末尾に「予測プロファイル」が表示されます。
2. 「予測プロファイル」の赤い三角ボタンをクリックし、[バギング予測の保存]を選択します。
3. 「ブートストラップ標本数」の横に「100」と入力します。
4. (オプション)「乱数シード値」に「2121」と入力します。
メモ: 無作為に復元抽出されるため、結果はいつも同じではありません。以下と同じ結果を再現するには、上記の「乱数シード値」を設定してください。
5. [OK]をクリックします。
データテーブルのウィンドウに戻ります。「予測式 <列名> バギング平均」、「標準誤差 <列名> バギング平均」、「<列名> バギング標準偏差」の3つの新しい列が追加されています。「予測式 <列名> バギング平均」列が、最終的な予測値です。
図3.32 バギングの後にデータテーブルに追加された列
予測値の比較
バギングによって予測能力が向上したかどうかを確認するために、バギングのモデルと元のモデルの予測値を比較してみましょう。「モデルの比較」プラットフォームを使用して、応答変数ごとに比較します。
1. [分析]>[予測モデル]>[モデルの比較]を選択します。
2. 「予測式摩擦 2」を選択し、[Y, 予測子]をクリックします。
3. 「予測式 摩擦 バギング平均」を選択し、[Y, 予測子]をクリックします。
4. [OK]をクリックします。
ウィンドウが開き、列名のリストが表示されます。
5. [摩擦]を選択して[OK]をクリックします。
6. 「モデルの比較」の赤い三角をクリックし、[予測値と実測値のプロット]を選択します。
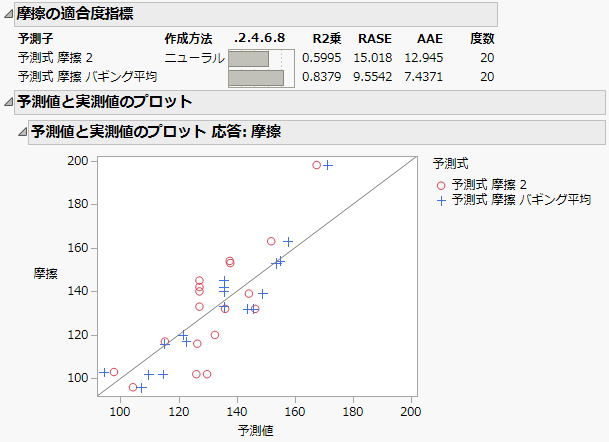
図3.33 「摩擦」に対する予測値の比較
「適合度指標」と「予測値と実測値のプロット」を、Figure 3.33に示します。バギングによる予測値は青で、元のニューラルネットワークモデルによる予測値は赤で示されています。全体的に見て、元のモデルよりもバギングの予測値のほうが、線の近くに位置しています。バギングの予測値のほうが線に近いため、その「R2乗」の値は0.8379と、元のモデルの値よりも大きくなっています。つまり、バギングによって「摩擦」の予測値が向上すると結論付けることができます。
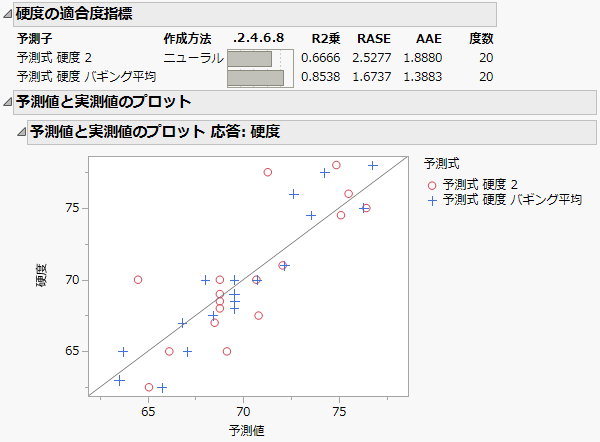
この例では、「摩擦」の予測値を比較しました。他の応答変数の予測値を比較するには、step 2からstep 6までの手順を繰り返してください。その際、「摩擦」を別の応答変数に変更します。Figure 3.34は、「硬度の適合度指標」レポートです。このレポートでも、「摩擦の適合度指標」レポートと同様の結果が導かれています。バギングの予測値の「R2乗」の値は、元のモデルの値よりもわずかに大きく、適合度が向上していることが示唆されています。
図3.34 「硬度」に対する予測値の比較