指数分布・Weibull分布・対数正規分布のプロットとあてはめ
「生存時間分析」プラットフォームでJMPがサポートしている3つの確率分布のそれぞれに、プロットとあてはめに関するコマンドが用意されています。まずプロットのコマンドを実行し、イベントを示す点が直線に沿うかどうか、つまり、その確率分布がよくあてはまっているかどうかを確かめてください。次にあてはめのコマンドを実行すると、パラメータの推定値が計算されます。
図14.5 指数プロット・Weibull・プロット・対数正規プロット
次の表では、何をプロットすれば確率分布が直線になるかを示しています。
確率プロット | 横軸 | 縦軸 | 解釈 |
|---|---|---|---|
指数分布 | 時間 | -log(S) | 傾きは1/θ |
Weibull分布 | log(時間) | log(-log(S)) | 傾きはβ |
対数正規分布 | log(時間) | Probit(1-S) | 傾きは1/σ |
メモ: Sは、Kapler-Meier法に基づく生存率の推定値です。
指数分布
指数分布は、イベントまでの時間データをモデリングするための最も単純な分布です。指数分布はθというパラメータだけを持ちます。指数分布はハザードが一定で、どれだけの時間を生存していたかがイベントの起こりやすさに影響しない分布です。パラメータθは寿命の期待値を表します。
Weibull分布
Weibull分布は、イベントまでの時間データをモデリングするための最もよく使われている分布です。Weibull分布としては、2パラメータのWeibull分布と、3パラメータのWeibull分布が有名です。「生存時間分析」プラットフォームは2パラメータのWeibull分布をあてはめます。Weibull分布の確率密度関数には、いくつかのパラメータ表現があります(Table 14.2)。JMPのレポートには2種類のパラメータ表現による結果が表示されます。1つはAlpha(α)とBeta(β)を使った「Weibullパラメータ推定値」、もう1つは最小極値分布に基づく「極値パラメータ推定値」です。
「Weibullパラメータ推定値」レポートに示されているαとβによるパラメータ表現は、信頼性分析の文献で広く使用されています(Nelson 1990)。パラメータαは、63.2%のユニットが故障する分位点を示します。パラメータβは、時間の経過と共にハザード(瞬間故障率)がどのように変化するかを決定します。βが1より大きい場合、ハザードは時間の経過とともに増加します。βが1より小さい場合、ハザードは時間の経過とともに減少します。βが1の場合、ハザードは一定になります。ハザードが一定であるWeibull分布は指数分布に等しくなります。
λとδを使った極値パラメータ化は、「極値パラメータ推定値」レポートに示されています。このパラメータ化は、Weibull分布を位置パラメータと尺度パラメータで表現しているので、統計的な意味で望ましい場合があります(Meeker and Escobar 1998, p. 86を参照)。位置パラメータはλ、尺度パラメータはδです。前述のαとβを用いたパラメータ表現との関係では、λはαの自然対数に等しく、δはβの逆数に等しくなっています。したがって、δパラメータは、時間の経過と共にハザードがどのように変化するかを決定します。δが1より大きい場合、ハザードは時間の経過とともに減少します。δが1より小さい場合、ハザードは時間の経過とともに増加します。δが1の場合、ハザードは一定になります。ハザードが一定であるWeibull分布は指数分布に等しくなります。
JMPにおけるWeibull分布 | α | β |
Wayne Nelson | alpha=α | beta=β |
Meeker and Escobar | eta=α | beta=β |
Tobias and Trindade | c = α | m = β |
Kececioglu | eta=α | beta=β |
Hosmer and Lemeshow | exp(X beta)=α | lambda=β |
Blishke and Murthy | beta=α | alpha=β |
Kalbfleisch and Prentice | lambda = 1/α | p = β |
JMPにおける極値分布 | lambda=log(α) | delta=1/β |
Meeker and Escobar s.e.v. | mu=log(α) | sigma=1/β |
対数正規分布
対数正規分布は、イベントまでの時間データをモデリングするための最も単純な分布です。対数正規分布では、値の対数をとったときの分布が正規分布になる分布です。つまり、逆に述べると、あるデータを指数変換したものに対数正規分布をあてはめることは、そのデータに正規分布をあてはめることと同じです。「生存時間(パラメトリック)のあてはめ」の別例を参照してください。
追加オプション
追加のオプションを表示するには、指数分布・Weibull分布・対数正規分布の各分布をあてはめるときに、Shiftキーを押しながら「Kaplan-Meier法によるあてはめ」の赤い三角ボタンをクリックし、希望のあてはめをクリックします。
これらのオプションによって、次のような計算や分析を行えます。
• 信頼限界の信頼水準を指定する。
• θ(指数分布の場合)、σ(対数正規分布の場合)、β(Weibull分布の場合)を特定の値に固定する。
WeiBayes分析を参照してください。
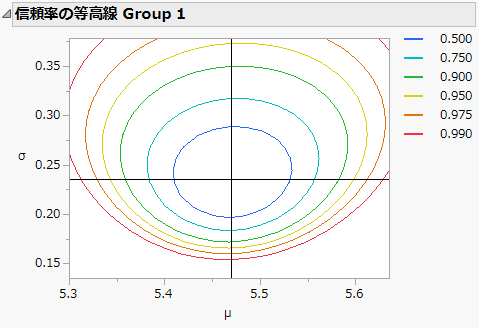
• Weibull分布および対数正規分布をあてはめたときに、信頼領域を表す等高線図を描く(いずれかのパラメータを特定の値に固定していない場合)。
図14.6 信頼率の等高線図
WeiBayes分析
JMPでは、指数分布をあてはめるときはθ、Weibull分布をあてはめるときはβ、対数正規分布をあてはめるときはσの各値を、特定の値に固定することができます。この機能は、以下のようなWeiBayesと呼ばれる状況で利用できます。
• 故障がまったくないか、ごく少ない
• 既知のβの値がある
• (さらに)βは既知だが、αの値は推定する必要がある
WeiBayes状況の詳細については、Abernethy(1996)を参照してください。
故障がまったくない場合、伝統的な古い手法では最後に故障データを加えて推定を行います。このように最後に故障を追加する方法は、ある種の下限値にはなっていますが、パラメータαを推定する妥当な方法ではありません。JMPのWeiBayes分析は、より妥当な推定方法となっています。