「直線のあてはめ」、「多項式のあてはめ」、「その他のあてはめ」レポート

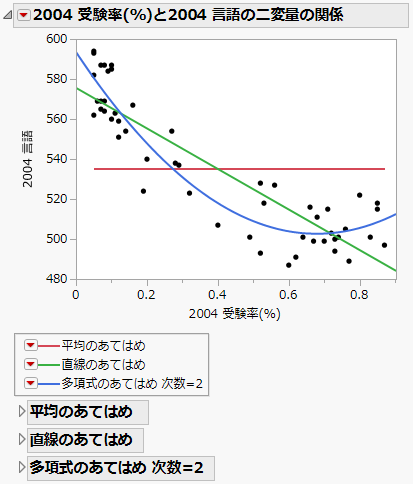
「二変量」プラットフォームの［直線のあてはめ］、［多項式のあてはめ］、［その他のあてはめ］は、回帰モデルをあてはめます。複数のモデルをあてはめて散布図上で比較することができます。

図5.8 直線や多項式のあてはめ 

［直線のあてはめ］メニューと［多項式のあてはめ］メニューのオプションについては、二変量の関係のオプションを参照してください。詳細については、［直線のあてはめ］オプションの統計的詳細を参照してください。

「二変量」プラットフォームでは、選択したあてはめのそれぞれにレポートが作成されます。「直線のあてはめ」、「多項式のあてはめ」、「変換されたあてはめ」の各レポートでは、テキストボックスの中にあてはめられた式が表示されます。各レポートは、あてはめの要約、分散分析（ANOVA）、パラメータ推定値で構成されます。データに反復がある場合は、あてはまりの悪さ（LOF; Lack Of Fit）の表も表示されます。変換したY変数のあてはめには、元のデータから計算した適合度指標の要約が含まれます。

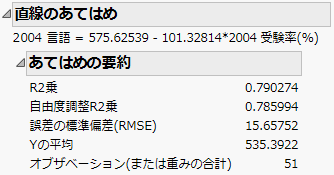
あてはめの要約

「二変量」プラットフォームのあてはめレポートには、モデルのあてはめの要約統計量をまとめた「あてはめの要約」表が表示されます。「あてはめの要約」表の上にあるのは、あてはめられた式です。

図5.9 「あてはめの要約」表 

「あてはめの要約」表には、次のような統計量が表示されます。

R2乗

モデルによって説明できる変動の割合を表します。残りの変動は、モデルで説明できないため、ランダムな誤差とみなされます。モデルが完全にあてはまっていると、R2乗は1になります。「あてはめの要約」レポートの統計的詳細を参照してください。

メモ: R2乗が小さい場合は、必要な説明変数がモデルに含まれていない可能性があります。ただし、扱っているデータの誤差やランダムな変動が大きい場合は、意味のある回帰モデルであっても、R2乗の値が小さくなることがあります。自分の研究分野の文献を読み、R2乗の大きさが通常、どれぐらいであるかを把握してください。

自由度調整R2乗

「自由度調整済みR2乗」、「自由度調整済み決定係数」などと呼ばれている指標であり、R2乗をモデルのパラメータ数で調整した指標です。自由度調整済みR2乗は、パラメータ数の異なるモデルを比較するのに役立ちます。「あてはめの要約」レポートの統計的詳細を参照してください。

誤差の標準偏差（RMSE）

誤差の標準偏差の推定値。これは、「分散分析」レポートにおける「誤差」行の「平均平方」列にある値の平方根です（Figure 5.11）。

Yの平均

応答変数の標本平均（算術平均）。これは、モデルで効果が指定されていないときのYの予測値です。

オブザベーション（または重みの合計）

モデルを推定するために使われた観測（オブザベーション）の個数。ただし、重み変数が使われた場合は、重みの合計です。

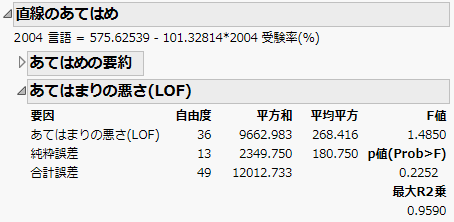
あてはまりの悪さ(LOF)

「二変量の関係」レポートの「あてはまりの悪さ(LOF)」表は、あてはまりの悪さ（Lack Of Fit）の検定結果を示します。あてはまりの悪さの検定は、X値に反復があり、モデルが飽和モデルでない場合のみ、可能です。反復から計算される平方和を、純粋誤差と呼びます。純粋誤差は、データの誤差のうち、どのようなモデルを構築しても説明や予測ができない変動を表します。

図5.10 「直線のあてはめ」の「あてはまりの悪さ(LOF)」表 

モデルの残差誤差から、純粋誤差を引いたものを、あてはまりの悪さ（LOF; Lack Of Fit）の誤差といいます。指定したモデルが不適切だと、LOF誤差が純粋誤差よりも有意に大きくなります。不適切なモデルとは、データを適切に描写していないモデルを指します。あてはまりの悪さ（LOF）検定の帰無仮説は、「母集団においてLOF誤差は0である」というものです。そのため、p値が小さいときは、モデルがデータにあてはまっていないことを意味します。

「あてはまりの悪さ(LOF)」表には、次のような列があります。

要因

変動の3つの要因（「あてはまりの悪さ(LOF)」、「純粋誤差」、「合計誤差」）。

自由度

誤差の各要因がもつ自由度（DF）。

– 「合計誤差」の自由度は、「分散分析」表の「誤差」の行に表示されている自由度です。分散分析を参照してください。「合計誤差」の自由度は、「分散分析」表の「全体」の自由度と「モデル」の自由度の差です。「誤差」の自由度は、あてはまりの悪さ（LOF）と純粋誤差の2つの自由度に分けることができます。

– 「純粋誤差」の自由度は、反復されている観測値の各グループにおける自由度を足し合わせた値です。「あてはまりの悪さ(LOF)」レポートの統計的詳細を参照してください。

– 「あてはまりの悪さ(LOF)」の自由度は、「合計誤差」と「純粋誤差」の自由度の差です。

平方和

誤差の各要因の平方和（SS）。

– 「合計誤差」の平方和は、「分散分析」表の「誤差」の行にある平方和です。分散分析を参照してください。

– 「純粋誤差」の平方和は、反復されている観測値の各グループにおける平方和を足し合わせた値です。この平方和を自由度で割った値は、モデルに依存しない、誤差分散の推定値になります。「あてはまりの悪さ(LOF)」レポートの統計的詳細を参照してください。

– 「あてはまりの悪さ(LOF)」の平方和は、「合計誤差」と「純粋誤差」の平方和の差です。LOFの平方和が大きいときは、モデルがデータに良くあてはまっていない可能性があります。

平均平方

要因の平均平方。平方和を自由度で割った値。「純粋誤差」の平均平方を基準にして、「あてはまりの悪さ(LOF)」の平均平方が相対的に大きくなっている場合、モデルがうまくあてはまっていないことを示します。F値を使って仮説検定を行うことができます。

F値

「あてはまりの悪さ(LOF)」の平均平方の、「純粋誤差」の平均平方に対する比。F値の値が大きいほど、「母集団においてLOF誤差は0である」という帰無仮説を否定する証拠が強いことを意味します。

p値(Prob > F)

あてはまりの悪さ（LOF）に対する検定のp値。検定の帰無仮説は、「母集団においてLOF誤差は0である」というものです。p値が小さいときは、現在のモデルがデータにあてはまっていないことを意味します。

最大R2乗

モデルに含まれている変数で達成できる最大のR2値。「あてはまりの悪さ(LOF)」レポートの統計的詳細を参照してください。

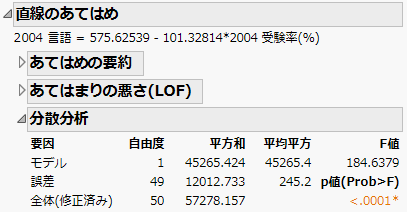
分散分析

「二変量の関係」レポートの「分散分析」表には、分散分析表が表示されます。分散分析表は、現在のモデルと切片だけのモデルとを比較した統計量で構成されています。「分散分析」表の値は、モデルの有効性を評価するF比の計算に使われます。「F値」に関連する確率（p値）が小さいとき、「そのモデルは、Yの平均だけのモデルよりも、良くあてはまっている」と見なすことができます。

図5.11 「直線のあてはめ」の「分散分析」表 

「分散分析」表には、次のような列があります。

要因

変動の3つの要因（「モデル」・「誤差」・「全体(修正済み)」）。

自由度

変動の各要因に関連した自由度（DF; Degrees of Freedom）。全体 全体の（修正済み）自由度は、標本サイズより常に1つ少なく、次のように「モデル」と「誤差」の自由度に分割されます。

– 「モデル」の自由度は、モデルのあてはめで使用されるパラメータの数（切片を除く）に相当します。

– 「誤差」の自由度は、「全体(修正済み)」と「モデル」の自由度の差です。

平方和

変動の各要因に関連した平方和（SS; Sum of Squares）。

– 全体（「全体(修正済み)」）の平方和は、各応答値から平均までの距離を2乗して合計したものです。これは、応答値の全体変動を示します。

– 「誤差」の平方和は、予測値から実測値までの距離の平方和です。これは、あてはめたモデルでは説明のつかない変動を示します。

– 「モデル」の平方和は、「全体(修正済み)」の平方和と「誤差」の平方和の差です。これは、モデルで説明される変動を示します。

平均平方

「誤差」と「モデル」における平均平方。平均平方は、平方和をその自由度で割った値です。

メモ: 「誤差」の平均平方の平方根は、「あてはめの要約」表にある「誤差の標準偏差(RMSE)」と同じです。

F値

モデルの平均平方を、誤差の平均平方（MSE; Mean Square for Error）で割った値。F値は、「現在のモデルが、切片だけのモデル（つまり、予測値が応答変数の平均値であるモデル）と有意に異なるかどうか」を検定するのに使われる検定統計量です。これは、「（切片を除く）すべての回帰パラメータが0である」という帰無仮説を検定します。この仮説が真のとき、「誤差」と「モデル」の平均平方は両方とも誤差分散の推定値となり、その比はF分布に従います。

p値(Prob > F)

検定の観測有意確率（p値）。p値が小さいと、回帰効果があると考えられます。

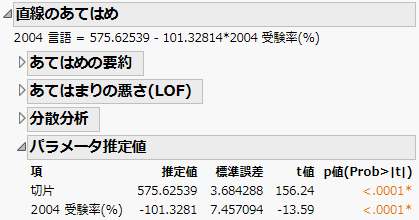
パラメータ推定値

「二変量の関係」レポートの「パラメータ推定値」表には、モデルのパラメータ推定値が表示されます。

図5.12 「直線のあてはめ」の「パラメータ推定値」表 

「パラメータ推定値」表には、以下の列があります。

項

パラメータ推定値に対応するモデル項。最初の項は切片です。

推定値

各項のパラメータ推定値。これらは、モデル係数の推定値です。

標準誤差

パラメータ推定値の標準誤差を推定した値。

t値

各パラメータがゼロであるという帰無仮説の検定統計量。t値は、パラメータ推定値とその標準誤差の比です。モデルに関する仮定が満たされるときは、このt値はStudentのt分布に従います。

p値(Prob>|t|)

「真のパラメータ値は0である」という帰無仮説、「真のパラメータ値は0ではない」という対立仮説の両側検定に対するp値。

追加の統計量を表示するには、レポートを右クリックし、［列］の各オプションを選択します。次の統計量はデフォルトでは表示されません。

下側95%

パラメータ推定値の両側95%信頼区間の下限。

上側95%

パラメータ推定値の両側95%信頼区間の上限。

標準β

すべての項を平均0、分散1に標準化したときの回帰モデルから得られるパラメータ推定値（標準化偏回帰係数）。「パラメータ推定値」レポートの統計的詳細を参照してください。

VIF

モデルの各項に対するVIF（Variance Inflation Factor）。この値が大きい場合、モデル内の項間に共線性があると考えられます。

計画の標準誤差

パラメータ推定値の相対分散の平方根。「パラメータ推定値」レポートの統計的詳細を参照してください。

元のスケールで測定したあてはめ

「二変量の関係」レポートの「元のスケールで測定したあてはめ」表には、変換前のスケールで測定した適合度の要約統計量が表示されます。この表は、Y変数を変換した場合のみ作成されます。