「多変量の相関」プラットフォームのオプション
「多変量」の赤い三角ボタンをクリックすると、次のようなオプションが表示されます。
相関係数行列
「相関」表の表示/非表示を切り替えます。この表は、相関係数を行列にしたもので、応答変数(Y)の各組み合わせに見られる線形関係の強さを示します。このオプションは、デフォルトでオンになっています。Pearsonの積率相関の統計的詳細を参照してください。
メモ: この相関係数行列は、起動ダイアログで指定した手法で計算されています。
相関のp値
「相関のp値」表の表示/非表示を切り替えます。この表は、p値の行列です。各p値は、「2つの変数間における母相関係数は0である」という帰無仮説に対する検定のp値です。この検定は、「2つの変数間には線形関係がない」という帰無仮説に対する検定にもなっています。この検定は、Pearsonの積率相関係数に対する検定です。
相関の信頼区間
相関係数に対する両側信頼区間の表示/非表示を切り替えます。
ヒント: デフォルトの信頼係数は95%ですが、[a水準の設定]オプションによって信頼係数を変更できます。
相関係数の逆行列
「相関の逆行列」レポート(相関係数行列の逆行列)の表示/非表示を切り替えます。相関係数行列の逆行列における対角要素は、該当する変数が他のすべての変数の線形関数によってどれぐらい説明されるかを表します。この対角要素の値は、1/(1 – R2)であり、R2は、他のすべての変数を説明変数とした線形重回帰分析から計算されます。その重相関係数が0のときは、対角要素は1となります。重相関係数が1のときは、対角要素は無限大になります(このときは、レポートでは欠測値になります)。相関係数行列の逆行列についての統計的詳細は、相関係数行列の逆行列を参照してください。
偏相関係数行列
「偏相関」レポート(偏相関係数行列)の表示/非表示を切り替えます。偏相関係数行列には、2変数の関係を他のすべての変数の効果で調整した偏相関が表示されます。偏相関係数行列は、相関係数行列の逆行列を、その対角要素が1になるように尺度化し、符号を逆にすることにより計算できます。
偏相関のp値
「偏相関のp値」レポート(p値の行列)の表示/非表示を切り替えます。各p値は、「2つの変数間における母偏相関係数は0である」という帰無仮説に対する検定のp値です。この検定は、「他のすべての変数の効果で調整した後、2つの変数間には線形関係がない」という帰無仮説に対する検定にもなっています。
メモ: [偏相関のp値]オプションは、自由度が足りない場合は使用できません。たとえば、観測数(標本サイズ、オブザベーションの個数)よりも変数が多い場合は、そうした状況になります。
共分散行列
共分散行列の表示/非表示を切り替えます。共分散行列は、2変数が一緒に変化する程度を表します。
ペアごとの相関係数
「ペアごとの相関係数」表の表示/非表示を切り替えます。この表には、ペアワイズ法によって計算されたPearsonの積率相関係数がリストされます。ペアワイズ法で欠測値を処理して計算が行われます。ペアになっている2変数のいずれかに欠測値がある場合は、その行は計算から除外されます。相関係数に対する有意確率も表示されます。また、相関の大きさが棒グラフで表されます。これらすべての結果はペアワイズ法に基づいて計算されます。
メモ: [ペアごとの相関係数]オプションでは、変数のペアのうちのいずれかが欠測値である行が計算から除外されます。
HotellingのT2検定
複数のY変数における平均に対し、1標本検定を実行します。このオプションを選択すると、帰無仮説の平均ベクトルを指定するためのウィンドウが開きます。そのウィンドウで、各 変数の仮説平均を入力してください。この検定は、Y変数が多変量正規分布に従うという仮定のもとで導出されています。「HotellingのT2検定」レポートには、以下の情報が表示されます。
変数
Y変数として指定した列。
平均
各変数の標本平均。
仮説平均
分析者が指定した、帰無仮説における平均。
検定統計量
HotellingのT2統計量の値。
F値
検定統計量の値。n個の行とk個の変数がある場合、F値は次のように表されます。
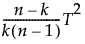
p値(Prob > F)
検定のp値。帰無仮説の下では、F値は、分子自由度kで分母自由度n - kのF分布に従います。
メモ: レポートを削除するには、「HotellingのT2検定」の赤い三角ボタンをクリックし、[検定結果の削除]を選択してください。
基本統計量
このメニューには2つのオプションがあり、それぞれが各列の基本統計量(平均・標準偏差・合計・最小値・最大値)の表示/非表示を切り替えます。欠測値がある場合やロバスト法が使用されているときには、単変量統計量と多変量統計量は異なった結果になります。
単変量の基本統計量
他の列の値や欠測値とは無関係に、各列で計算された統計量が表示されます。これらの値は、「一変量の分布」プラットフォームで算出される値と一致します。
多変量の基本統計量
起動ウィンドウで選択した分散推定法に従って計算された統計量が表示されます。データに欠測値がない場合、推定法として[ロバスト] 法を選択した場合にだけこのオプションを選択できます。データに欠測値がある場合には、[ペアワイズ]以外のすべての分散推定法でこのオプションを使用できます。[REML]法・[最尤]法・[ロバスト]法においては、それらの選択した推定法により平均ベクトルと共分散行列が推定されます。[リストワイズ]法では、1つでも欠測値のある行は計算から除外した後に、1変数ごとの平均と分散が計算されます。
ノンパラメトリック相関係数
[ノンパラメトリック相関係数]のサブメニューにはノンパラメトリックな指標(ペアごとの相関係数)があります。各オプションを選択すると、ノンパラメトリック相関係数のレポートが開き、それらの相関係数に対するp値も表示されます。また、相関係数の大きさが棒グラフで表示されます。3種類のノンパラメトリック相関係数は以下のとおりです。
Spearmanの順位相関係数
データ値そのものではなく、データ値を順位に置き換えて計算した相関係数です。
Kendallの順位相関係数
大小関係が一致するペアと一致しないペアの個数から計算された相関係数です。データから2行を取り出して比較したときに、Xが大きい方が、Yも大きくなっているペアを、大小関係が一致するペアといいます。逆に、Xが大きい方が、Yが小さくなっているペアを、大小関係が一致しないペアといいます。なお同順位のペア(XまたはYの値が等しいペア)がある場合、それらの影響も考慮して、修正された値が計算されます。
HoeffdingのD統計量
–0.5~1の値を取る指標です。値が正で大きいほど従属性が高いことを示します。この統計量は、2×2の分割表から計算されたカイ2乗統計量の重み付き和の近似値です。その2×2の分割表は、各データ値を閾値として作成されます。この指標は、独立性からの全体的な乖離を検出します。
メモ: ノンパラメトリックな相関係数は、起動ウィンドウで別の分散推定法を指定した場合でも、常にペアワイズ法によって計算されます。
メモ: [重み]変数を指定した場合、その重みが欠測値および0である行は、ノンパラメトリックな相関係数の計算から除外されます。その他の重みの値はすべて1として扱われます。
これら3種類のノンパラメトリックな相関係数に関する詳細については、ノンパラメトリックな関連の指標の統計的詳細を参照してください。
a水準の設定
相関係数に対する信頼区間のα水準(有意水準)を変更できます。サブメニューには、[0.01]・[0.05]・[0.10]・[0.50]の4つの値が表示されています。それ以外の値を入力したい場合は[その他]を選択してください。
散布図行列
散布図行列の表示/非表示を切り替えます。散布図行列とは、応答変数の各ペアに対する散布図を行列形式で表したものです。このオプションは、デフォルトでオンになっています。散布図行列を参照してください。
カラーマップ
[カラーマップ]メニューには数種類のカラーマップがあります。いずれも、それぞれのカラーマップの表示/非表示を切り替えます。カラーマップの種類には、以下のものがあります。
相関のカラーマップ
相関係数を、赤色~青色(-1~+1)で表したセルプロットが作成されます。
p値のカラーマップ
相関係数に対するp値を、赤色(p = 0)から青色(p = 1)で描いたセルプロットが作成されます。
相関のクラスタリング
似ている変数をまとめたセルプロットが作成されます。「相関のカラーマップ」と相関係数自体(セルの色)は変わりませんが、変数の位置が異なる場合があります。
ペアごとの相関係数のカラーマップ
ペアごとの相関係数を、赤色~青色(-1~+1)で表したセルプロットが作成されます。
Spearmanの順位相関(r)のカラーマップ
Spearmanのノンパラメトリックな相関係数(r)を、赤色~青色(-1~+1)で表したセルプロットが作成されます。
Kendallの順位相関(t)のカラーマップ
Kendallのノンパラメトリックな相関係数(t)を、赤色~青色(-1~+1)で表したセルプロットが作成されます。
HoeffdingのD統計量のカラーマップ
Hoeffdingのノンパラメトリックな相関係数(D統計量)を、赤色~青色(-1~+1)で表したセルプロットが作成されます。
パラレルプロット
パラレルプロットの表示/非表示を切り替えます。
三次元楕円プロット
95%確率楕円体も描かれている3次元散布図の表示/非表示を切り替えます。このオプションを選択すると、3つの変数とその軸を指定するためのウィンドウが表示されます。
偏相関図
偏相関図レポートの表示/非表示を切り替えます。このオプションは、偏相関行列の大きさを視覚的に表現します。デフォルトの配置には固有値分解した結果が使われます。図の表示を変更するオプションがいくつかあります。偏相関図を参照してください。
外れ値分析
このメニューに含まれるオプションは、Mahalanobisの距離、ジャックナイフ法による距離、またはT2のいずれかの手法を使って、変数間の相関を考慮して計算された中心からの距離をプロットしたグラフの表示/非表示を切り替えます。外れ値分析を参照してください。
項目の信頼性
このメニューのオプションは、「項目の信頼性」レポートの表示/非表示を切り替えます。「項目の信頼性」レポートは、複数の測定項目(変数の組)において、どれほど一貫した測定ができているかを示します。Cronbachのa係数と、標準化した変数に対するCronbachのa係数の2種類が用意されています。項目の信頼性を参照してください。
欠測データの補完
(データテーブルに欠測値がある場合のみ使用できます。)元のデータテーブルにおける欠測値を推定値に置き換えて、データテーブルを新規に作成します。各行の非欠測値から計算された条件付き期待値によって、欠測値は補完されます。起動ウィンドウで指定した推定方法によって平均ベクトルと共分散行列が推定され、それによって条件付き期待値が算出されます。欠測値が補完されたデータセットを用いれば、あらゆる種類の多変量検定や多変量分析を実行できます。
欠測データ補完の計算式を保存
(データテーブルに欠測値がある場合のみ使用できます。)欠測値を含む列に関して、欠測値の推定に使用した計算式を、データテーブル内の新しい列に保存します。新しい列には、「補完された_<列名>」という名前がつきます。
以下のオプションの詳細については、『JMPの使用法』の「JMPレポートのローカルデータフィルタ」、「JMPレポートの[やり直し]メニュー」、および「JMPレポートの[スクリプトの保存]メニュー」を参照してください。
ローカルデータフィルタ
データをフィルタリングするためのローカルデータフィルタの表示/非表示を切り替えます。
やり直し
分析を繰り返したり、やり直したりするオプションを含みます。また、[自動再計算]オプションに対応しているプラットフォームにおいては、[自動再計算]オプションを選択すると、データテーブルに加えた変更が、該当するレポートに即座に反映されるようになります。
プラットフォーム環境設定
現在のプラットフォームの環境設定を表示したり、現在のJMPレポートの設定に合わせて環境設定を変更したりできます。
スクリプトの保存
レポートを再現するためのスクリプトを保存するオプションが、保存先ごとに用意されています。
Byグループのスクリプトを保存
By変数の全水準に対するレポートを再現するスクリプトを保存するオプションが、保存先ごとに用意されています。起動ウィンドウでBy変数を指定した場合のみ使用可能です。