変数重要度の統計的詳細
ここでは、予測プロファイルにおける変数重要度の計算方法について説明します。
計算方法
予測モデルを表す関数を、fとします。また、モデルの因子(入力変数)を、x1, x2, ..., xnとします。
y = f(x1, x2 ..., xn)という関係が成り立っているとします。
• yの期待値E(y)は、x1, x2, ..., xnの同時分布において、それらの変数でyを積分したものです。
• yの分散Var(y)は、x1, x2, ..., xnの同時分布において、それらの変数で(y – E(y))2を積分したものです。
主効果
xjのyに対する主効果を、Var(E(y |xj))と定義します。この定義において、まず、xjが与えられたときの条件付き期待値を求め、そして、その条件付き期待値の分散をxjの周辺分布から求めます。言い換えると、Var(E(y |xj))は、「xjが与えられたときのyの条件付き平均」の分散になっています。
次に、主効果xjに対するyの感度(sensitivity)を、Var(E(y |xj))/Var(y)という比率によって定義します。「要約レポート」の「主効果」列に示される変数重要度は、乱数シミュレーションによってこの比率を推定した値です(標本抽出に伴う誤差の調整を参照)。
全効果
「全効果」は、xjにかかわるすべての項による、y = f(x1, x2 ..., xn)の分散への寄与全体を表します。全効果の計算は、関数的分解に基づいています。関数的分解では、関数fが、定数および1変数だけからなる項、複数の変数を組み合わせた項などを示す関数に分解されます。このように分解された成分は、分散分析における主効果、交互作用や高次の効果に相当します。Saltelli(2002)、Sobol(1993)を参照してください。
xjの全効果を計算するにあたっては、まず、分解された成分のうち、xjを含む項が識別されます。そして、それらの各項について、条件付き期待値の分散が計算されます。その後、それら各項の条件付き期待値の分散は合計されます。この合計値は、xjを含む複数の項が、Var(y)に対して、全体としてどれぐらい寄与しているかを示します。各xjについて、これらの値は、ユーザによって選択された、入力変数のシミュレーション方法に基づいて算出されます。こうして算出された値は、「全効果」という列に表示されます(標本抽出に伴う誤差の調整も参照してください)。
x1とx2という2因子しかない簡単な場合で、全効果の重要度がどのように算出されるか考えてみましょう。
x1が関係する全効果の重要度は、次式で算出されます。
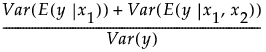
標本抽出に伴う誤差の調整
「要約レポート」の「主効果」と「全効果」に出力される推定値は、標本抽出によって算出されているため、誤差が生じます。その標本抽出の誤差は、次に述べる方法で調整される場合があります。「全効果」が、「主効果」より小さくなった場合は、「全効果」が「主効果」と等しい値に設定されます。また、「主効果」の合計が1より大きくなる場合は、合計が1になるように値が正規化されます。
変数重要度の標準誤差
入力変数に対して独立性を仮定した場合には、重要度の標準誤差が計算されます。この標準誤差は、モンテカルロ法の計算精度を表すものです。重要度の計算において、この標準誤差は以下のように使われます。
• ラテン超方格法によって、データを複数組、生成します。
• データの各組ごとに、主効果と全効果の重要度を計算します。
• この重要度に対する標準誤差の推定値が、全因子について閾値の0.01を下回るまで、上記の計算が繰り返されます。
レポートに表示される標準誤差は、反復計算が終了した時点での標準誤差です。