等分散性の検定レポート
「一元配置」プラットフォームには、4種類の等分散性の検定があります。等分散性の検定のうちの3つは、各グループ内でのばらつきを測定するための新しいY変数を作成し、それに対して分散分析を行います。もう1つはBartlettの検定です。Bartlettの検定は、正規分布のもとでの尤度比検定に類似しています。起動ウィンドウでブロック変数を指定した場合、［等分散性の検定］オプションは使用できません。
メモ: 等分散性の検定としては、分散の平均分析（ANOMV）法も使用できます。平均分析レポートを参照してください。
等分散性の検定として、以下のものが用意されています。
O’Brien
グループ平均が元のY変数のグループごとの不偏分散と等しくなるような従属変数が新しく作成されます。O’Brien検定は、グループごとの分散に対する分散分析と言えます（O’Brien 1979; Olejnik and Algina 1987）。
Brown-Forsythe
各グループにおける中央値と各観測値との差の絶対値を応答として分散分析を実行し、F検定を行います（Brown and Forsythe 1974）。
Levene
各グループにおける平均と各観測値との差の絶対値を応答として分散分析を実行し、F検定を行います（Levene 1960）。ばらつきは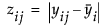
として計算されます。
Bartlett
標本分散の重み付きの算術平均を、標本分散の重み付きの幾何平均と比べます。幾何平均は必ず算術平均以下になり、算術平均と幾何平均が等しくなるのは、すべての値が等しい場合です。すべての標本分散が等しいと、それらの算術平均と幾何平均は等しくなります。グループごとの分散の間に見られる変動が大きいほど、2つの平均の差が大きくなります。2つの平均から計算された値が、c2分布によって近似されます（カイ2乗分布は、F分布の分母自由度を無限大にし、分子自由度を掛けたものです）。カイ2乗検定統計量の値が大きいということは、算術平均／幾何平均の比が大きい、つまりグループごとの分散の違いが大きいことを意味します。Bartlett検定のカイ2乗検定統計量を自由度で割ったものが、F値として出力されます。Bartlettの検定は、正規性の仮定が満たされないケースに対してロバスト（頑健）ではありません（Bartlett and Kendall 1946）。
両側F検定
（X変数の水準数が2水準の場合にのみ使用可能）検定の対象が2つのグループだけである場合、等分散性の検定として標準的なF検定も行われます。F検定は、小さい方の分散値に対する大きい方の分散推定値の比です。両側検定にする目的で、F分布のp値に2が掛けられます。
メモ: ブロック列を指定した場合は、分散検定を行う前に、データがブロック平均に合わせて調整されます。
等分散性検定の例を参照してください。
ヒント: 等分散性の検定からグループの分散が有意に異なることがわかったときは、通常のANOVA検定ではなく、Welchの検定を使用した方がよいかもしれません。Welchの統計量は、通常の一元配置分散分析におけるF検定の枠組みを用いていますが、グループごとの不偏分散の逆数で加重された平均が計算に使われています（Welch 1951; Brown and Forsythe 1974; Asiribo and Gurland 1990）。水準が2つしかないとき、Welchの一元配置分散分析は分散が等しくない場合のt検定と等価です。
「分散が等しいことを調べる検定」レポート
「一元配置」プラットフォームの「分散が等しいことを調べる検定」レポートには、標準偏差のプロットと要約表が表示されます。最初の表には以下の列があります。
水準
因子の水準。
度数
各水準の度数。
標準偏差
X変数の水準ごとの応答変数の標準偏差。O’Brien検定における変換された変数のグループ平均は、標準偏差の2乗（分散）です。データが1つしかない水準については、標準偏差は計算されません。
平均からの平均絶対偏差
グループ平均からの偏差の絶対値を平均した値。Levene検定における変換された変数のグループ平均は、それらの絶対偏差を平均したものです。
中央値からの平均絶対偏差
グループ中央値からのYの偏差の絶対値を平均した値。Brown-Forsythe検定における変換された変数のグループ平均は、それらの絶対偏差を平均したものです。
2つ目の表は、等分散性の検定をまとめたもので、次の列があります。
検定
各検定の名前。
F値
計算されたF統計量。等分散性検定の統計的詳細を参照してください。
分子自由度
分子で使用される自由度。因子の水準数をkとすると、分子にはk-1個の自由度があります。O’Brien、Brown-Forsythe、およびLeveneの統計量の計算では、データが1つしかない水準は無視されます。その場合の分子自由度は、計算に使用された水準数からさらに1を引いたものになります。
分母自由度
分母で使用される自由度。O’Brien、Brown-Forsythe、およびLeveneでは、検定統計量の計算に使用された因子水準の数だけ自由度が引かれます。因子の水準数をkとすると、分母自由度はn - kとなります。
p値
「分散がすべての水準にわたって等しい」という仮定のもとで、現在のF値より大きなF値を得る確率。
メモ: X変数のいずれかの水準で標本サイズが5に満たない場合は、警告が表示されます。標本サイズが小さいときの上記の検定の性能については、Brown and Forsythe（1974）とMiller（1972）を参照してください。
「Welchの検定」レポート
F値
平均が等しいかどうかを調べる検定のF統計量。
分子自由度
検定の分子で使用される自由度。因子の水準数をkとすると、分子にはk-1個の自由度があります。標本サイズが1しかない水準は、Welchの一元配置分散分析の計算には使用されません。その場合の分子自由度は、計算に使用された水準数からさらに1を引いたものになります。
分母自由度
検定の分母で使用される自由度。等分散性検定の統計的詳細を参照してください。
p値(Prob>F)
「母平均がすべての水準において等しい」という仮定のもとで、現在のF値より大きなF値を得る確率。
t検定
（X変数の水準数が2水準の場合のみ使用できます。）F値とt値の関係を示すために出力されます。t値は、F値の平方根です。