1つの予測変数による回帰分析
Y変数が連続尺度で、連続尺度のX変数が1つある場合は、単回帰モデルをあてはめることができます。
シナリオ
この例では、会社情報のサンプルデータ「Companies.jmp」を用います。このデータには、製薬業界とコンピュータ業界における32社の財務データが記録されています。
従業員数が多い会社の方が、従業員数が少ない会社よりも売上が多いことは、直感的にもうなずけます。データアナリストは、各社の総売上を従業員数に基づいて予測しようと考えています。
そのためには、次の作業を行います。
• 関係の洗い出し
• 平均売上の予測
関係の洗い出し
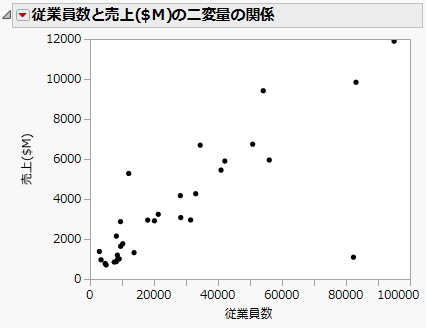
まず、散布図を作成し、従業員数と売上の関係を確認します。この散布図は、「散布図の作成」ですでに作成しました。1つの外れ値(従業員数と売上が他社より抜きん出ている会社)を非表示にし、かつ除外した後の散布図をFigure 5.12に示します。
図5.12 「売上($M)」と「従業員数」の散布図
この散布図は、売上と従業員数間の関係を明確に示しています。直感どおりに、従業員数が多い会社ほど売上が高くなっています。この散布図は、データアナリストの直感を視覚的に裏付けてはいます。しかし、この散布図だけからは、ある従業員数に対する売上高の予測値を決めることができません。
回帰モデルをあてはめる
従業員数から売上を予測するには、回帰モデルをあてはめます。「二変量の関係」の赤い三角ボタンをクリックし、[直線のあてはめ]を選択します。散布図に回帰直線が追加され、新しいレポートがレポートウィンドウに追加されます。
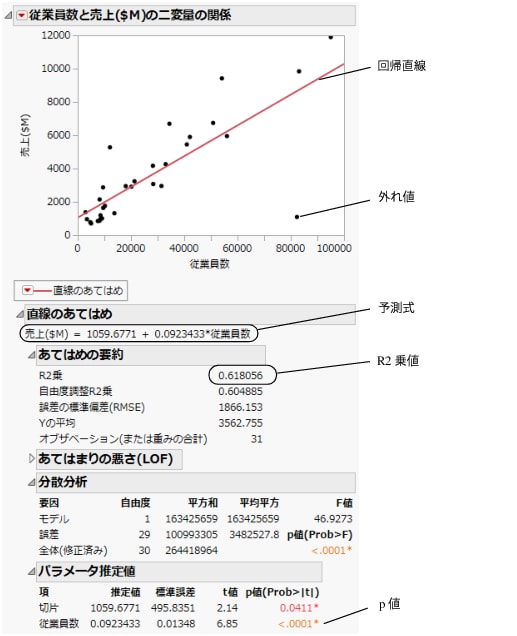
図5.13 回帰直線
レポート内で次の結果に着目してください。
• p値< 0.0001
• R2乗値 = 0.618
これらの結果から、次の結果を導き出せます。
• モデル項「従業員数」のp値は小さい値になっています。これは、有意水準0.05において「従業員数」の係数がゼロでないことを示します。つまり、予測モデルに従業員数を含めると、売上の平均を予測する度合いが有意に向上するということです。
• R2乗の0.618という値は、このモデルが売上の変動のおよそ62%を説明していることを意味します。R2乗値は、決定係数であり、従属(応答)変数の変動のうち、どれだけをモデルが説明しているかを示します。R2乗値の範囲は0~1です。R2乗値が0の場合、そのモデルには説明する力がないことを表します。R2乗値が1の場合、そのモデルは応答を完璧に予測します。
平均売上の予測
回帰モデルによって、所定数の従業員を擁する会社の平均売上を予測します。レポートには、次のモデルの予測式が示されています。
平均売上 = 1059.68 + 0.092*従業員数
たとえば、従業員数が70,000人の会社の場合、売上はおよそ7,500ドルと予測されます。
7,499.68 = 1059.68 + 0.092 x 70,000
現在の散布図の右下部分に、他社が示す一般的なパターンに合致しない外れ値があります。この外れ値を除外した場合に予測モデルが変化するかどうかを確認する必要があります。
外れ値の除外
1. 外れ値をクリックします。
2. [行]>[除外する/除外しない]を選択します。
3. このモデルをあてはめるには、「従業員数と売上($M)の二変量の関係」の赤い三角ボタンをクリックし、メニューから[直線のあてはめ]を選択します。
レポートウィンドウに次の情報が追加されます(Figure 5.14を参照)。
• 新しい回帰直線。
• 新しい「直線のあてはめ」レポート。次の情報が表示されます。
– 新しい予測式
– 新しいR2乗値
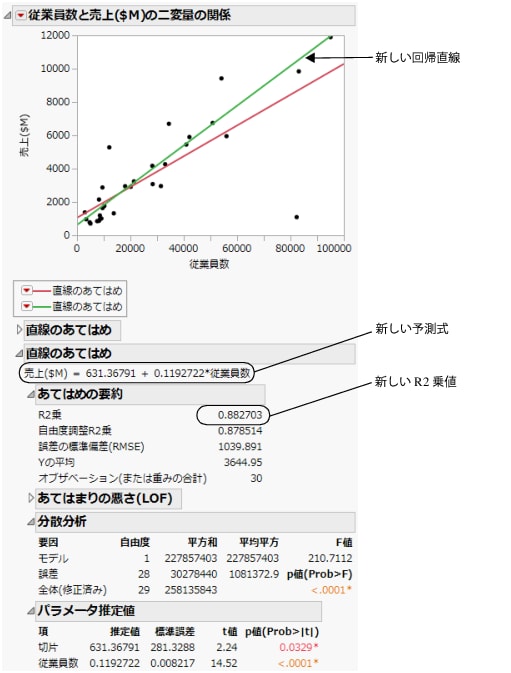
図5.14 モデルの比較
結果の解釈
Figure 5.14の結果を参考に、次の結論を導き出すことができます。
• 回帰直線は、外れ値によって大規模企業側で引き下げられ、小規模企業側で引き上げられていました。
• データから外れ値を除外して新たにあてはめたモデルは、最初のモデルよりあてはまりが良いと言えます。新しいモデルのR2乗値は0.88で、最初のモデルの値より高く、1に近くなっています。
結論の導き出し
新しい予測式を使用すると、従業員が70,000人の会社の平均売上は、次のように予測されます。
8961.37 = 631.37 + 0.119 x 70,000
最初のモデルによる予測値は、約7500ドルでした。2番目のモデルで予測される売上は約8960ドルで、最初のモデルに比べて1460ドル増加しています。
外れ値を除外した後の2番目のモデルの方が、最初のモデルと比べて、より良く売上を説明および予測しているようです。これで、使用すべき良いモデルを求めることができました。