하나의 예측 변수가 있는 회귀 사용
연속형 Y 변수와 단일 연속형 X 변수가 있는 경우 단순 회귀 모형을 생성할 수 있습니다.
시나리오
이 예에서는 제약 및 컴퓨터 업계의 32개 회사에 대한 재무 데이터가 포함된 Companies.jmp 데이터 테이블을 사용합니다.
직원 수가 많은 회사가 직원 수가 적은 회사보다 많은 매출 수익을 창출한다는 것은 직관적으로 알 수 있습니다. 데이터 분석가는 직원 수에 따라 각 회사의 전체 매출 수익을 예측하려고 합니다.
이 작업을 완수하려면 다음을 수행하십시오.
• 관계 발견
• 회귀 모형 적합
• 평균 매출 예측
관계 발견
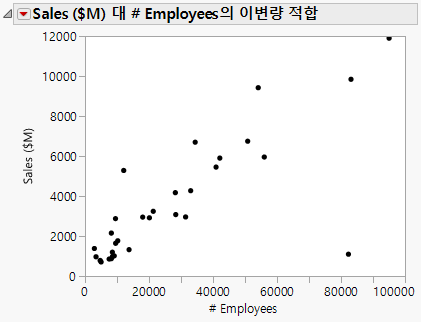
먼저, 직원 수와 매출 수익 간의 관계를 확인하기 위해 산점도를 생성합니다. 이 산점도는 "산점도 생성"에서 생성되었습니다. 그림 5.12의 산점도는 여기에서 이상치 하나(직원 수와 매출이 현저하게 높은 회사)를 숨기고 제외한 후의 결과를 보여 줍니다.
그림 5.12 Sales ($M) 대 # Employ 산점도
이 산점도는 매출과 직원 수 간의 관계를 명확하게 보여 줍니다. 예상대로, 회사의 직원이 많을수록 매출액이 높아질 수 있습니다. 이 산점도로 데이터 분석가의 추측을 시각적으로 확인할 수 있지만 특정 수의 직원에 대한 매출을 예측할 수는 없습니다.
회귀 모형 적합
직원 수로 매출 수익을 예측하려면 회귀 모형을 적합시켜야 합니다. "이변량 적합"의 빨간색 삼각형을 클릭하고 선형 적합을 선택합니다. 산점도에 회귀선이 추가되고 보고서 창에 보고서가 추가됩니다.
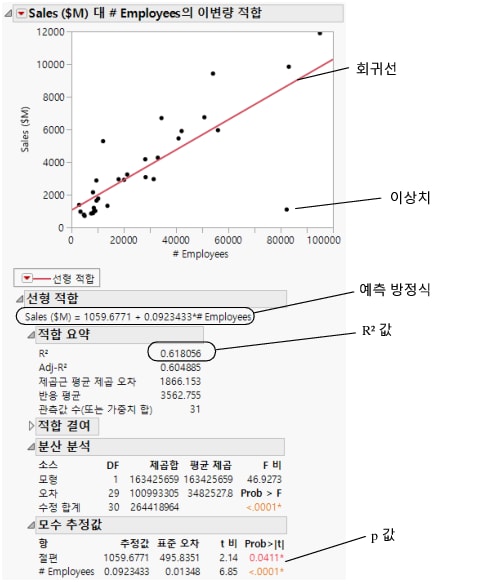
그림 5.13 회귀선
보고서에서 다음 결과를 확인하십시오.
• p 값이 .0001보다 작음
• R² 값이 0.618임
이러한 결과를 바탕으로 데이터 분석가는 다음과 같은 결론을 내릴 수 있습니다.
• "# Employ" 모형 항의 p 값이 작습니다. 이는 유의 수준 0.05에서 "# Employ"에 대한 계수가 0이 아니라는 것을 뒷받침합니다. 따라서 예측 모형에 직원 수를 포함하면 직원 수가 포함되지 않은 모형에 비해 평균 매출을 예측하는 능력이 크게 향상됩니다.
• R² 값 0.618은 이 모형이 매출 변동의 약 62%를 설명하고 있음을 나타냅니다. R² 값은 결정 계수로서, 모형으로 설명되는 종속(반응) 변수의 분산 비율을 나타냅니다. R²는 0에서 1 사이입니다. R²가 0인 모형은 설명력이 없습니다. R²가 1인 모형은 반응을 완벽하게 예측합니다.
평균 매출 예측
회귀 모형을 사용하면 특정 수의 직원이 있을 때 회사에서 기대할 수 있는 평균 매출을 예측할 수 있습니다. 이 모형에 대한 예측 방정식이 보고서에 포함되어 있습니다.
평균 매출 = 1059.68 + 0.092*직원 수
예를 들어 직원 수가 70,000명인 회사의 매출은 약 7,500달러로 예측됩니다.
7,499.68달러 = 1059.68 + 0.092*70,000
현재 산점도의 오른쪽 아래에는 다른 회사의 일반적인 패턴을 따르지 않는 이상치가 있습니다. 데이터 분석가는 이 이상치가 제외될 때 예측 모형이 바뀌는지에 대해 알고 싶습니다.
이상치 제외
1. 이상치를 클릭합니다.
2. 행 > 제외/제외 해제를 선택합니다.
3. 이 모형을 적합시키려면 "Sales (SM) 대 # Employ의 이변량 적합" 옆의 빨간색 삼각형을 클릭하고 선형 적합을 선택합니다.
다음 항목이 보고서 창에 추가됩니다(그림 5.14).
• 새 회귀선
• 다음을 포함하는 새 선형 적합 보고서
– 새 예측 방정식
– 새 R² 값
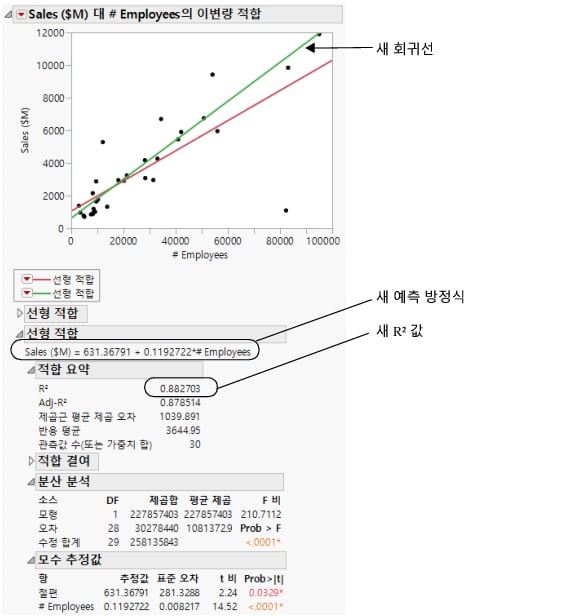
그림 5.14 모형 비교
결과 해석
그림 5.14의 결과를 바탕으로 데이터 분석가는 다음과 같은 결론을 내릴 수 있습니다.
• 이상치는 큰 회사의 회귀선을 끌어내리고 작은 회사의 회귀선을 끌어올립니다.
• 이상치가 없는 데이터에 대한 새 모형은 첫 번째 모형보다 강력한 모형입니다. 새 R² 값 0.88은 초기 분석보다 높고 1에 더 가깝습니다.
결론
새 예측 방정식을 사용하면 7만 명의 직원이 있는 회사의 예측 평균 매출을 다음과 같이 계산할 수 있습니다.
8,961.37달러 = 631.37 + 0.119*70,000
첫 번째 모형의 예측값은 약 7,500달러입니다. 두 번째 모형에서는 총 매출을 첫 번째 모형에 비해 1,460달러 늘어난 약 8,960달러로 예측합니다.
이상치를 제거한 두 번째 모형은 직원 수를 기준으로 한 매출 총액을 첫 번째 모형보다 더욱 정확하게 설명하고 예측합니다. 데이터 분석가는 이제 사용하기 적절한 모형을 확보했습니다.