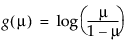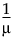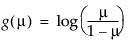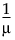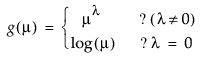广义线性模型构造的统计详细信息

拟合线性模型 > 广义线性模型 > “广义线性模型”特质的统计详细信息 > 广义线性模型构造的统计详细信息

发布日期: 09/18/2023

广义线性模型构造的统计详细信息

要构造广义线性模型，您必须为数据选择响应变量和解释变量。然后为响应选择合适的连结函数和概率分布。解释变量可以是连续变量、分类变量和交互作用的任意组合。表 13.1 中列出了一些常见的广义线性模型示例。

表 13.1 广义线性模型的示例
模型	响应变量	分布	默认连结函数
传统线性模型	连续	正态	恒等，g(m) = m
Logistic 回归	计数或二值随机变量	二项	logit，
对数线性模型中的 Poisson 回归	计数	Poisson	对数，g(m) = log(m)
指数回归	连续（正数）	指数

平台通过参数向量的最大似然估计用广义线性模型来拟合数据。通常对于参数的最大似然估计值没有闭合形式的解。因此，平台使用 Nelder and Wedderburn (1972) 最早提出的一个方法通过迭代拟合过程在数字上估计模型的参数。通过用 Pearson 拟合优度统计量除以其自由度来估计过度离散参数 f。基于最大似然估计量的渐近正态性计算估计参数的协方差、标准误差和置信限。

在“拟合模型”平台的“广义线性模型”特质中提供很多连结函数和概率分布。表 13.2 列出了内置连结函数。

表 13.2 内置连结函数
连结函数名称	连结函数公式
恒等	g(m) = m
Logit
Probit	g(m) = F-1(m)，其中 F 是标准正态累积分布函数
对数	g(m) = log(m)
倒数	g(m) =
幂
互补重对数	g(m) = log(–log(1 – m))

选择“幂”连结函数时，显示一个数字框，允许您输入所需的幂。

表 13.3 列出与该响应变量的可用分布关联的方差函数。

表 13.3 响应分布的方差函数
分布	方差函数
正态	V(m) = 1
二项	V(m) = m(1 – m)
Poisson	V(m) = m
指数	V(m) = m2

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).