该帮助的版本不再更新，请参见https://www.jmp.com/support/help/zh-cn/15.2 获取最新的版本.


实验设计指南  • 混料设计 • 混料设计类型的示例 • 极端顶点设计
上一个
 • 
下一个
极端顶点设计
极端顶点设计需要对一个或多个因子的范围进行限制，这由“因子”面板中的限值或线性约束来指定。极端顶点设计包含因子空间顶点处的混料和指定次数的顶点平均值处的混料。由一条线连接的两个邻近顶点的重心点为二次重心。共享一个平面的顶点的重心点为三次重心。
包含范围约束的极端顶点示例
要创建一个示例极端顶点设计，请执行以下步骤：
1.
选择实验设计 > 经典 > 混料设计。
2.
在“因子”下，输入 2 作为要添加的其他因子数，然后点击添加。
3.
如图 13.12中所示设置五个因子的范围，然后点击继续。
图 13.12 五个因子的范围
4.
在次数文本框中输入 4，然后点击极端顶点设计。
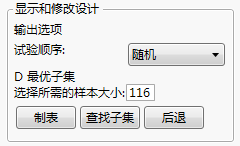
图 13.13 极端顶点设计示例的“显示和修改”面板
这个五个因子、次数为 4 的极端顶点设计的默认试验次数为 116。这是在给定范围约束的条件下五个因子的极端顶点数和次数为 4 的平均数。JMP 使用混料的默认集作为候选集来生成更小的 D 最优设计。
5.
（可选）要匹配该示例的输出，请点击“混料设计”红色小三角并选择“设置随机种子”，然后输入 1409。
6.
在“选择所需的样本大小”框中输入 10，然后点击查找子集来生成设计。
注意：查找子集选项使用行交换方法（不是坐标交换）来查找最佳行子集。
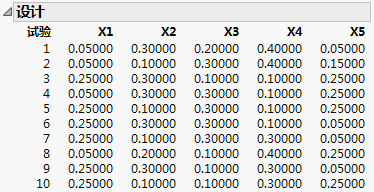
图 13.14 试验次数为 10 的最优极端顶点设计
7.
点击制表。
直观演示设计
8.
从设计表中，选择图形 >三元图。
9.
选择 X1、X2、X3、X4 和 X5，点击 X，绘图，然后点击确定。
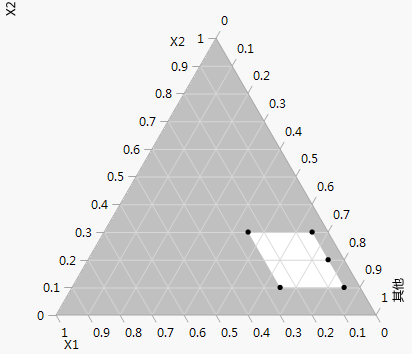
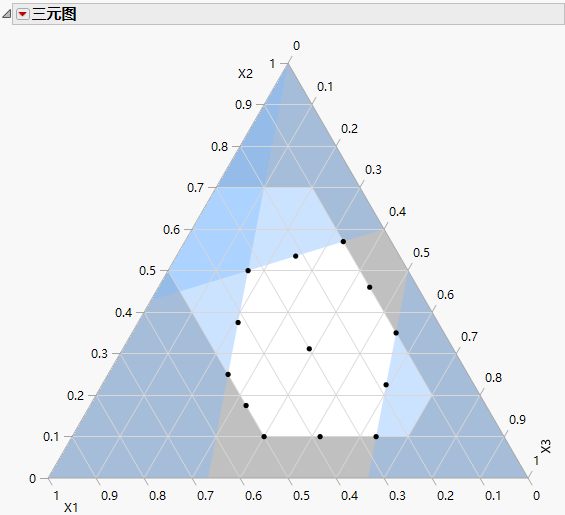
图 13.15 五因子设计的三元图的部分输出
当您有三个以上的混料成分时，三元图显示一系列图。每个图具有两个成分轴，第三个轴是所有其他成分之和。若您有受约束的区域，则将这些图着色。未着色的部分为可行域。有关三元图的详细信息，请参见三元图概述。
包含线性约束的极端顶点示例
考虑 Snee (1979) 和 Piepel (1988) 提供的经典示例。该示例具有三个因子（X1、X2 和 X3），且具有因子边界和三个线性约束。
要为该示例创建极端顶点设计，请执行以下步骤：
1.
选择实验设计 > 经典 > 混料设计。
2.
为 X1、X2 和 X3 输入图 13.16中的值，然后点击继续。
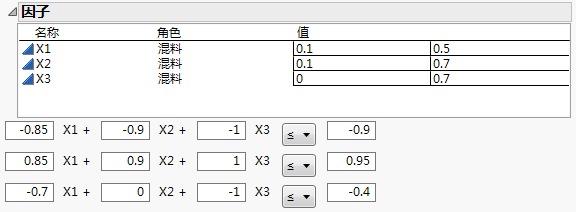
图 13.16 Snee 和 Piepel 示例的值和线性约束
3.
点击三次线性约束。输入图 13.16中所示的约束。
4.
点击极端顶点设计按钮。
5.
点击制表。
直观演示设计
6.
从设计表，选择图形 > 三元图。
7.
选择 X1、X2 和 X3 并点击 X，绘图，然后点击确定。
图 13.17 显示带有约束的 Piepel 示例的三元图
三元图显示因子限值和线性约束所定义的可行域。设计点位于可行域的六个顶点、六边的中点和整体重心。有关三元图的详细信息，请参见三元图概述。
极端顶点方法的统计详细信息
若存在线性约束，JMP 使用 R.E. Wheeler 开发的 CONSIM 算法，该算法在 Snee (1979) 中进行了说明，由 Piepel (1988) 作为 CONVRT 提供。该方法在 Cornell (1990, Appendix 10a) 中也有说明。方法中结合了约束和检查，以查看顶点是否与它们冲突。若冲突，它会删除顶点并计算新顶点。用来计算重心点的名为 CONAEV 的方法是由 Piepel (1988) 提出的。
若不存在线性约束（只有范围约束），则会使用 Snee and Marquardt (1974) 以及 Snee (1975) 开发的 XVERT 方法构造极端顶点设计。找到顶点之后，单纯形重心设计方法会生成直到指定阶数的顶点组合。
XVERT 方法首先使用具有最小范围的 nf – 1 个因子的给定低值和高值创建完整的 2nf – 1 设计。然后，它根据因子值总和必须为 1 的限制计算剔除的一个因子的值。它保留不在因子范围之内的点。若不在范围之内，该方法会增大或减小该值使其位于范围之内，并且相应地让其他每个因子的值减小或增大相同的量。该方法使这些点仍满足最初的限制。
上述算法可在因子约束定义的单纯形中创建可行域的顶点。不过，Snee (1975) 已证明具有可行域的边和面的重心也会很有用。可行域的广义 n 维面通过 nf – n 条边界来定义，而面的重心通过落在面上的顶点的平均值来定义。该算法生成边界条件的所有可能组合，然后对第一步生成的顶点取平均值。