使用该选项可获取用来比较模型效应各水平所定义的均值的检验和置信水平。多重比较方法的目标是:确定组均值是否存在差异,同时控制得出不正确结论的概率。“多重比较”选项支持您将组均值与总平均值(均值分析)和控制组均值进行比较。您还可以使用 Tukey HSD 或 Student t 执行配对比较。指定 Student t 方法时,还可以执行等价性检验来识别有实际意义的配对差值。
“多重比较”选项的控制窗口示例显示在图 3.28中。本例基于 Big Class.jmp 数据表,其中将体重设置为 Y,年龄、性别和身高设置为模型效应。有两类估计值可用于比较:“最小二乘均值估计值”和“用户定义的估计值”。
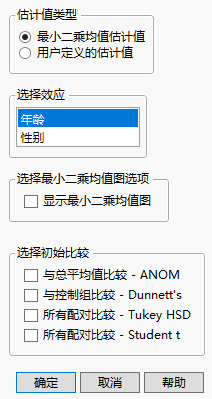
该选项比较最小二乘均值,仅在模型中有名义型或有序型效应时才可用。回想一下,最小二乘均值是在模型中其他效应设置为某个中性值时计算的均值。(有关最小二乘均值的定义,请参见最小二乘均值表。)您必须选择相关的效应。在图 3.28中,为年龄指定了“最小二乘均值估计值”。提供显示最小二乘均值图的选项。请参见最小二乘均值图选项。
图 3.28 “最小二乘均值估计值”的启动窗口
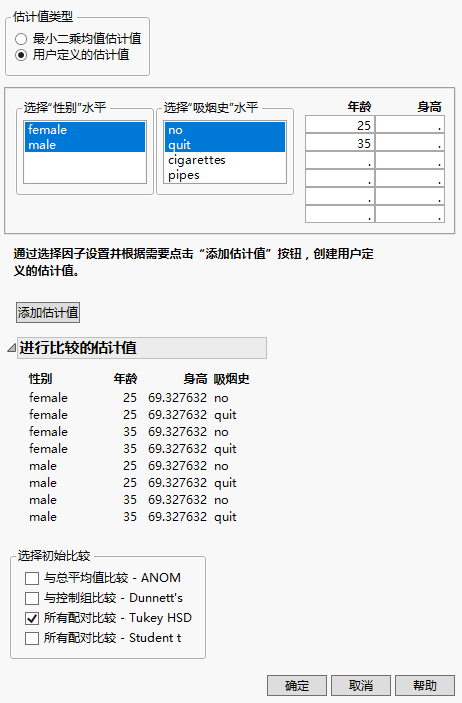
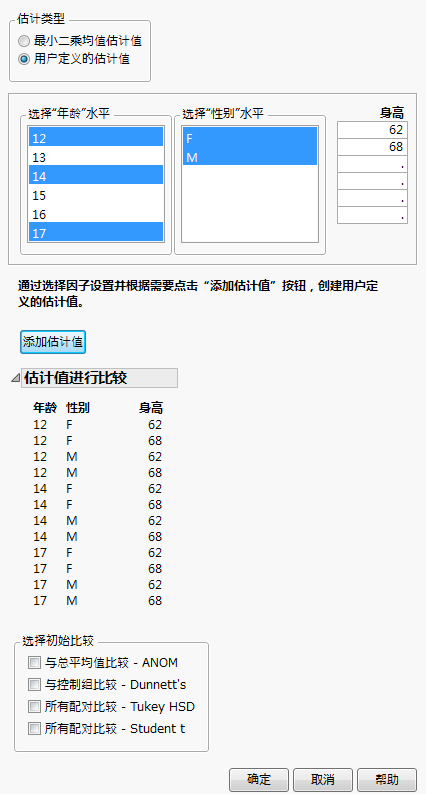
图 3.29对如何指定“用户定义的估计值”进行了演示。已选定“年龄”的三个水平和“性别”的两个水平。此外,还手动输入了“身高”的两个值。已点击“添加估计值”按钮,生成了指定水平的所有可能组合的列表。此时,您可以指定更多估计值,并通过再次点击“估计值”按钮将其添加至“估计值进行比较”列表。
图 3.29 “用户定义的估计值”的启动窗口
显著性检验的 t 比。仅当您在报表中右击并选择“列”>“t 比”时才显示该列。
显著性检验的 p 值。仅当您在报表中右击并选择“列”>“概率>|t|”时才显示该列。
该选项将指定水平的均值与这些水平的总均值进行比较。它显示一个表(其中显示总均值差值的置信区间)和一个图(其中显示决策限)。比较所用的方法称为均值分析(ANOM) (Nelson et al. 2005)。ANOM 是一种多重比较过程,用来控制针对总均值的所有配对比较的联合误差率。有关基于 Lipid Data.jmp 样本数据表的报表,请参见图 3.30。
用于构造决策限的 Nelson h 统计量的值。
具体而言,平均最小二乘均值是权重与矩阵 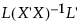 的对角线元素成反比的加权平均值。其中,L 是用于计算组最小二乘均值的系数所构成的矩阵。有关最小二乘均值和平均最小二乘均值的技术定义,请参见《SAS/STAT 14.3 用户指南》中的“GLM 过程”一节 (SAS Institute Inc. 2017)。
的对角线元素成反比的加权平均值。其中,L 是用于计算组最小二乘均值的系数所构成的矩阵。有关最小二乘均值和平均最小二乘均值的技术定义,请参见《SAS/STAT 14.3 用户指南》中的“GLM 过程”一节 (SAS Institute Inc. 2017)。
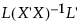 的对角线元素成反比的加权平均值。其中,L 是用于计算组最小二乘均值的系数所构成的矩阵。有关最小二乘均值和平均最小二乘均值的技术定义,请参见《SAS/STAT 14.3 用户指南》中的“GLM 过程”一节 (SAS Institute Inc. 2017)。
的对角线元素成反比的加权平均值。其中,L 是用于计算组最小二乘均值的系数所构成的矩阵。有关最小二乘均值和平均最小二乘均值的技术定义,请参见《SAS/STAT 14.3 用户指南》中的“GLM 过程”一节 (SAS Institute Inc. 2017)。对于用户定义的估计值,平均均值也按类似方式定义。不过,在这种情况下 L 是用于定义估计值的系数所构成的矩阵。
|
‒
|
Nelson:提供精确临界值和 p 值。尽可能使用,特别是在估计值不相关时。
|
|
‒
|
|
•
|
|
•
|
将包含 p 值(概率>|t|)的列添加到“与总平均值比较”报表。请注意,计算不平衡设计的精确临界值和 p 值要求复积分,计算起来可能较为困难。针对此类分位数的计算若失败,则计算 Sidak 分位数,但不提供 p 值。
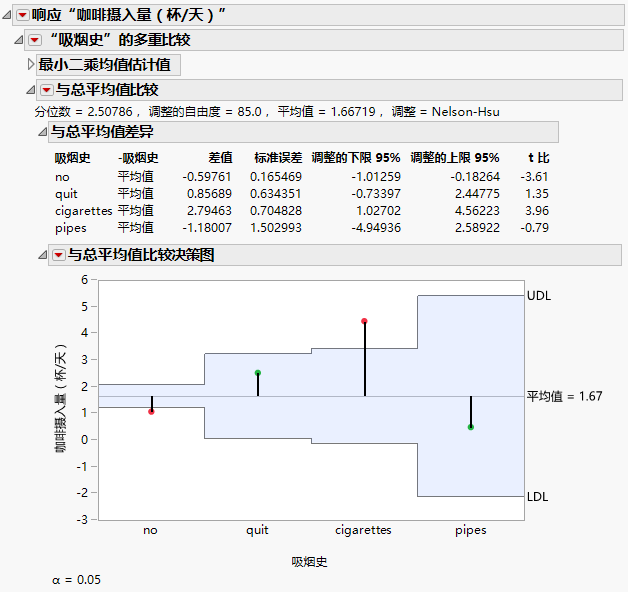
考虑 Lipid Data.jmp 样本数据表。您关注在控制饮酒状况和心脏病史的前提下四种吸烟史类别中是否有任何类别的咖啡摄入量(杯/天)均值与咖啡摄入量的总平均值有明显不同。您指定包含咖啡摄入量(杯/天)的模型作为响应,将吸烟史、饮酒状况和心脏病史作为模型效应。
|
1.
|
|
2.
|
选择分析 > 拟合模型。
|
|
3.
|
|
4.
|
|
5.
|
点击运行。
|
|
6.
|
从“响应‘咖啡摄入量(杯/天)’”旁边的红色小三角菜单中,选择估计值 > 多重比较。
|
|
7.
|
从“选择效应”列表中,选择吸烟史。
|
|
8.
|
在“选择初始比较”列表中,选择与总平均值比较 - ANOM。
|
|
9.
|
点击确定。
|
图 3.30 与“分级”的总平均值比较
若选择“与控制组比较 - Dunnett’s”,随即打开一个窗口,要求您指定控制组。若选定“最小二乘均值估计值”,该列表将包含您选定的效应的所有水平。若选定“用户定义的估计值”,该列表将包含您指定的效应水平组合。
选择控制组并点击“确定”后,“与控制组比较”报表随即显示在“拟合最小二乘法”报表中。该选项比较指定设置的均值与控制组均值。它显示一个表(其中显示与控制组差值的置信区间)和一个显示决策限的图。使用 Dunnett 方法进行比较。Dunnett 方法是一种多重比较过程,用于控制所有比较上的误差率 (Hsu 1996; Westfall et al. 2011)。
若无法精确计算 p 值和置信区间,则使用 Hsu 因子分析近似 (Hsu 1992)。请注意,计算不平衡设计的精确临界值和 p 值要求复积分,可能需要大量计算。针对此类分位数的计算若失败,则计算 Sidak 分位数。
|
‒
|
Dunnett:提供精确临界值和 p 值。尽可能使用,特别是在估计值不相关时。
|
|
‒
|
|
•
|
|
•
|
将包含 p 值(概率>|t|)的列添加到“与总平均值比较”报表。请注意,计算不平衡设计的精确临界值和 p 值要求复积分,计算起来可能较为困难。针对此类分位数的计算若失败,则计算 Sidak 分位数,但不提供 p 值。
“所有配对比较”选项可显示“Tukey HSD 所有配对比较”或“Student t 所有配对比较”报表 (Hsu 1996; Westfall et al. 2011)。构造 Tukey HSD 比较,以使显著性水平联合应用到所有配对比较。相比之下,对于 Student t 比较,显著性水平应用到每一单个比较。使用 Student t 检验执行若干配对比较时,某个比较被错误地判定存在差异的风险可能远远超出规定的显著性水平。
检验的临界值。请注意,对于 Tukey HSD,分位数为 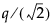 ,其中 q 是适当的学生化范围统计量的百分点。
,其中 q 是适当的学生化范围统计量的百分点。
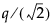 ,其中 q 是适当的学生化范围统计量的百分点。
,其中 q 是适当的学生化范围统计量的百分点。|
‒
|
Tukey:提供精确临界值和 p 值。在均值不相关且具有相等方差时或设计的方差平衡时使用。
|
|
‒
|
Tukey-Kramer:提供近似临界值和 p 值。在无法获取精确值时使用。
|
Tukey HSD 和 Student t 比较所有水平对。对于每个配对比较,“所有配对差异”报表都显示:
|
•
|
|
•
|
|
•
|
概率>|t| — 检验的 p 值
|
使用该选项可执行一个或多个等价性检验。若您想要检测有实际意义的差值,等价性检验很有用。您需要为组均值指定一个阈值差,比这更小的差值可被视为实际上等价。换言之,若两个组均值的差值未超过该数值,您愿意将其视为等价。
双单侧检验 (TOST) 方法用于检验均值之间的实际差值 (Schuirmann 1987)。针对实际差值超过阈值的原假设,构造双单侧合并方差 t 检验。若两个检验都拒绝,则均值差值在统计上未超过任一阈值。因此,这些组被视为实际上等价。若只有一个检验拒绝或两个检验均未拒绝,则各组可能实际上不等价。
|
•
|
t 比下限、t 比上限 — 双单侧合并方差显著性检验的 t 比的下限和上限
|
|
•
|
|
•
|
最大 p 值 — p 值下限和上限的最大值
|
考虑 Lipid Data.jmp 样本数据表。您关注在两个年龄组(25 和 35 岁)和平均身高保持不变的情况下胆固醇是否存在性别差异,是否在非吸烟者和曾吸烟者(其吸烟史分别等于 no 和 quit)方面存在差异。
|
1.
|
|
2.
|
选择分析 > 拟合模型。
|
|
3.
|
|
4.
|
|
5.
|
点击运行。
|
|
6.
|
从“响应‘胆固醇’”旁边的红色小三角菜单,选择估计值 > 多重比较。
|
|
7.
|
从“估计值类型”列表中,点击用户定义的估计值。
|
|
8.
|
|
9.
|
|
10.
|
在年龄列表中,在前两行输入年龄 25 和 35。
|
|
11.
|
点击添加估计值。
|
|
12.
|
在“选择初始比较”列表中,选择所有配对比较 - Tukey HSD。
|
图 3.31 已填写的“用户定义的估计值”窗口
|
13.
|
点击确定。
|
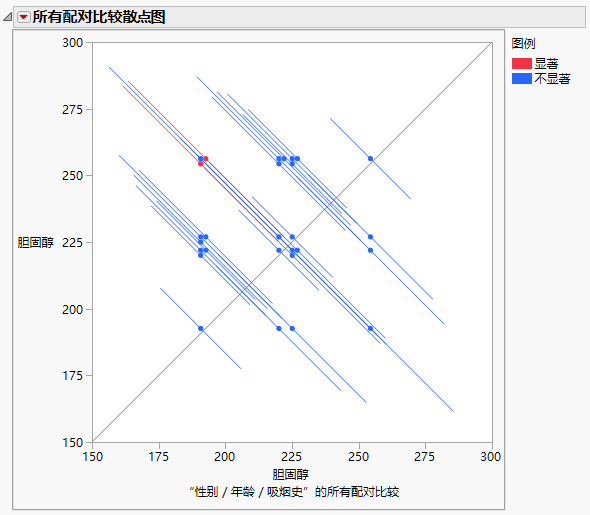
“所有配对差值”报表指示 28 个配对比较中的 2 个是显著的。图 3.32中显示的“所有配对比较散点图”将这些比较的置信区间显示为红色。您可以将光标置于任何点上以确定该点代表哪个配对比较。工具提示还包含该比较中两个水平的差值。图 3.32中的两个红色点表示对男性和女性比较 35 岁的曾吸烟者和 25 岁的非吸烟者的点。
图 3.32 针对用户定义的比较的“所有配对比较散点图”
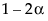 置信区间的上下限
置信区间的上下限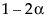 置信区间。线段上的点的坐标是对应组的均值。将光标置于其中一个点上会显示工具提示,指示要比较的组并显示估计差值。若线段完全包含在对角带内,由此判定均值实际上等价。
置信区间。线段上的点的坐标是对应组的均值。将光标置于其中一个点上会显示工具提示,指示要比较的组并显示估计差值。若线段完全包含在对角带内,由此判定均值实际上等价。