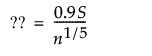图 11.14 单项详细报表
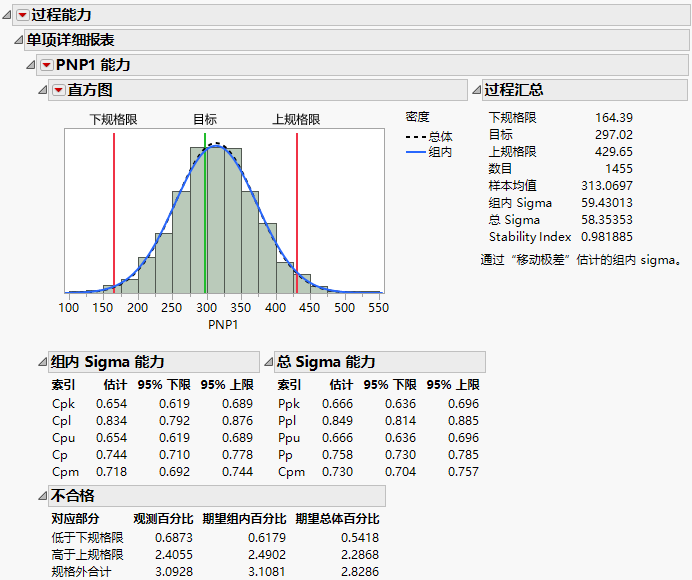
具有正态分布的某变量的“单项详细报表”显示直方图、过程汇总详细信息,以及能力和不合格统计量。该直方图显示值的分布、上规格限、下规格限和过程目标(若已指定),以及显示假设分布的一条或两条曲线。图 11.14中的直方图显示两条正态曲线 — 一条基于标准差的总估计值,另一条基于子组内估计值。
使用正态分布拟合过程时,“过程汇总”包括稳定性比,这是一个用于衡量过程稳定性的测度。稳定性比定义如下:
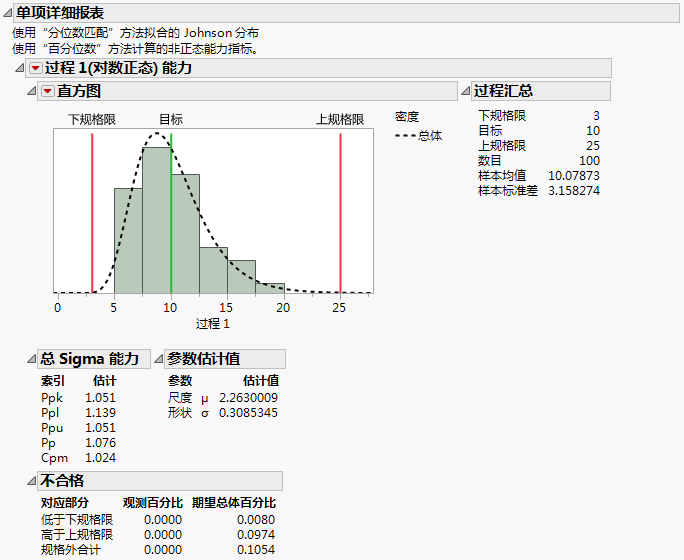
图 11.15 过程 1 的“单项详细报表”
非正态分布的能力指标:百分位数和 Z 得分方法中对用于正态、beta、指数、gamma、Johnson、对数正态和 Weibull 分布的参数和概率密度函数进行了说明。以上这些也是“分布”平台中使用的参数化,只不过“过程能力”不支持阈值参数。请参见《基本分析》手册中的“分布”。
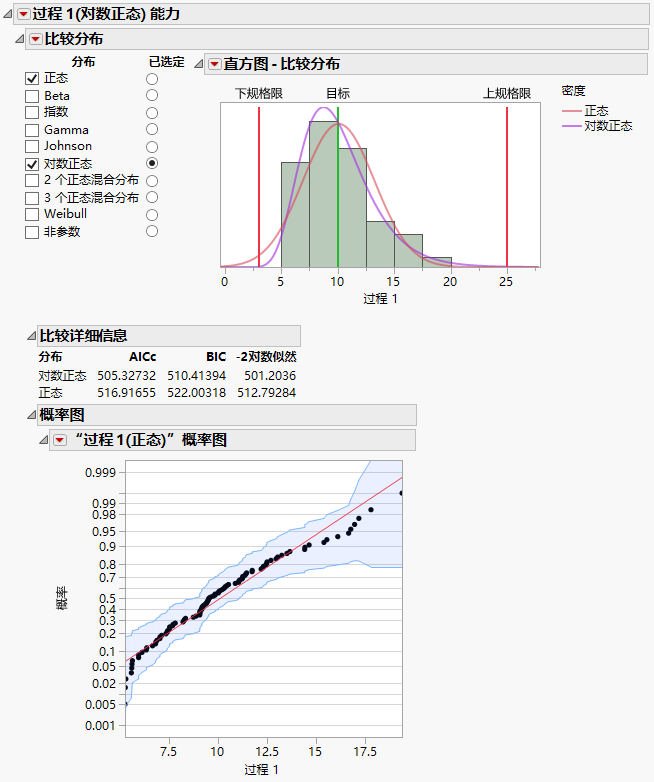
图 11.16显示 Process Measurements.jmp 样本数据表中过程 1 的“比较分布”报表。“已选定”分布(即“对数正态”)正与“正态”分布作比较。“比较详细信息”报表显示这两种分布的拟合统计量。
通过从“比较分布”红色小三角菜单中选择“概率图”选项,您可以获取概率图。图 11.16中正态分布的概率图中的各点并未紧贴线条分布。这表示拟合不佳。
图 11.16 比较带有正态概率图的分布
显示或隐藏为您拟合的每个参数分布显示概率图的报表。请参见图 11.16。观测的水平坐标是其观测的数据值。观测的垂直坐标是观测秩的拟合分布的分位数值。对于正态分布,总 sigma 估计值用于确定拟合分布。
在数据来自选定参数系列的前提下,显示或隐藏有联合 95% 置信水平包含真概率函数的置信限。这些限值在所有点处都包含相同的估计精度。用这些值来确定选定的参数分布是否能够很好地拟合数据。请参见 Nair (1984) 和 Meeker and Escobar (1998)。
若可能,通过将参数分布 F 表示为位置尺度系列来计算区间,以便 F(y) = G(z),其中,z = (y - μ)/σ。使用 delta 方法来计算拟合位置尺度分量在某点处的近似标准误差。使用标准误差估计值,将为每个点计算 z 的 Wald 置信区间。累积分布函数 F 的置信区间通过使用 G 变换 Wald 区间得到。请注意,在某些情况下,需要特别调整以便在过程测量值区间端点附近提供适当区间。