Example of a Response Surface Design
Use the Response Surface Design platform to construct a Box-Behnken design for three factors. You want to experiment over a wide range of factor settings to find the settings that achieve a target.
Construct a Box-Behnken Design
1. Select DOE > Classical > Response Surface Design.
2. Select Help > Sample Data Folder and open Design Experiment/Bounce Response.jmp.
3. Click the Response Surface Design red triangle and select Load Responses.
4. Select Help > Sample Data Folder and open Design Experiment/Bounce Factors.jmp.
5. Click the Response Surface Design red triangle and select Load Factors.
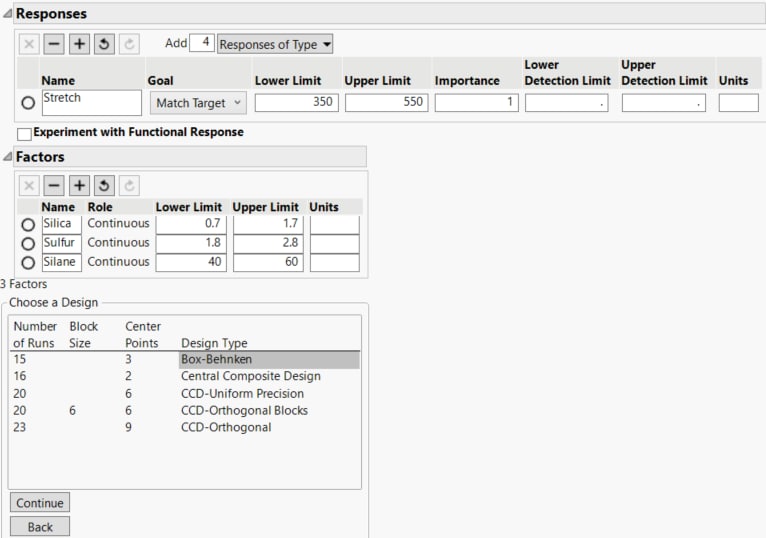
Figure 12.4 Responses and Factors for Tire Tread Design
In the Responses section, notice that the Goal for Stretch is set to Match Target.
In the Choose a Design panel, possible designs appear.
Note: Setting the Random Seed in step 6 reproduces the exact results shown in this example. In constructing a design on your own, this step is not necessary.
6. (Optional) Click the Response Surface Design red triangle and select Set Random Seed. Type 12345 and click OK.
7. Click Continue to retain the Box-Behnken design selection.
8. Click Make Table.
At this point, conduct the experiment and enter the responses into the data table.
Analyze the Experimental Data
1. Select Help > Sample Data Folder and open Design Experiment/Bounce Data.jmp.
The file Bounce Data.jmp contains your experiment results.
2. Run the Model script.
Notice that the main effects in the Construct Model Effects list are followed by the & RS suffix. This suffix indicates that these are response surface effects, which produce a Response Surface report in the Standard Least Squares report.
3. Click Run.
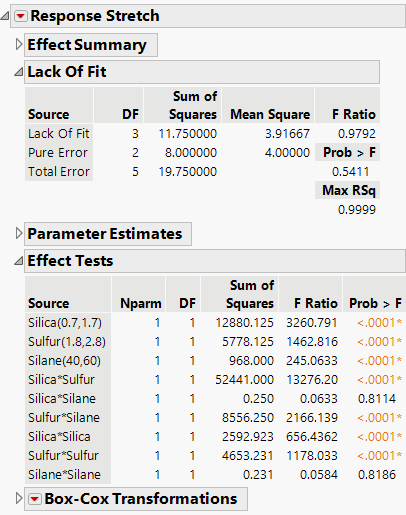
Figure 12.5 Lack of Fit and Effect Tests Reports
There is no indication of lack of fit and the Effect Tests report indicates that all but two higher-order terms (Silica*Silane and Silane*Silane) have p-values below 0.0001. See “Lack of Fit” and “Effect Tests” in Fitting Linear Models for more information about interpretation of the tables in Figure 12.5.
4. Click the disclosure icon next to Response Surface to open the report.
5. Click the disclosure icon next to Canonical Curvature.
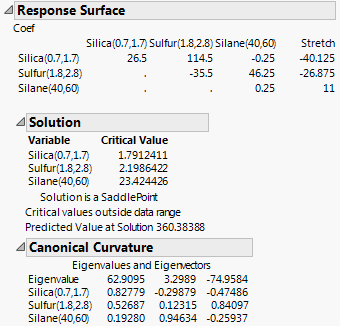
Figure 12.6 Response Surface Report
The Coef table shown as the first part of the report gives a concise summary of the estimated model parameters. The first three columns give the coefficients of the second-order terms. The last column gives the coefficients of the linear terms. To see the prediction expression in its entirely, select Estimates > Show Prediction Expression from the Response Stretch red triangle.
The Solution report gives the coordinates of the point where the single critical value occurs. In this instance, that point is a saddle point (a point where neither a maximum nor a minimum occurs) and falls outside the range of the design space.
The Canonical Curvature report shows eigenvalues and eigenvectors of the effects. These give information about the nature and direction of the surface’s curvature. The large positive eigenvalue of 62.9095 indicates positive curvature and the eigenvector values indicate that the curvature is primarily in the Silica direction. The large negative eigenvalue of -74.9584 indicates negative curvature and the eigenvector values indicate that the curvature is primarily in the Sulfur direction.
See Example of a Response Surface Model in Fitting Linear Models for more information about the response surface analysis tables in Figure 12.6.
Next, use the prediction profiler and the contour profiler to find optimal settings.
Explore Optimal Settings
1. Click the Prediction Profiler red triangle and select Optimization and Desirability > Maximize Desirability.
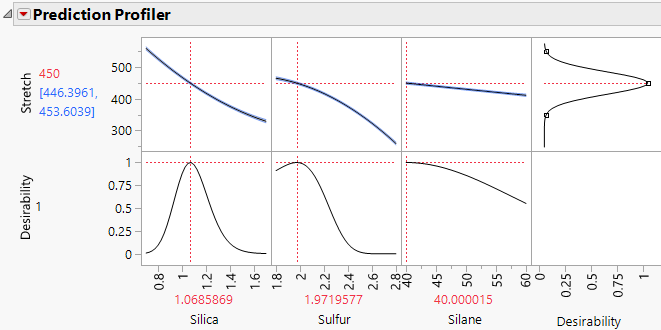
Figure 12.7 Prediction Profiler for Bounce Data.jmp with Desirability Maximized
Note: Your optimal settings might differ. This is because there are many points for which the predicted Stretch is 450.
When you specified the response, the goal was set to match a target of 450, with lower and upper limits of 350 and 550. This goal was carried over to the design table and these limits were put in a Response Limits column property for Stretch. A desirability function is constructed from these response limits (top right cell in Figure 12.7). See Response Limits.
When you maximize the desirability function, JMP identifies one combination of factor level settings (usually out of many possible combinations) that results in a predicted Stretch of 450. Figure 12.7 shows these settings as Silica = 1.069, Sulfur = 1.972, and Silane = 40.000. Next, you use the Contour Profiler to identify other points that maximize the desirability function.
For more information about the Prediction Profiler, see Profiler inProfilers.
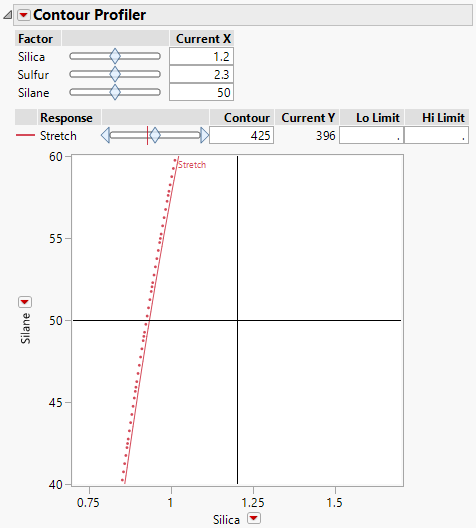
2. Click the Response Stretch red triangle and select Factor Profiling > Contour Profiler. Suppose that you want to achieve your target while setting Sulfur to the value 2.0. Also, you want to make sure that the settings that you choose for Silane and Silica maintain predicted Stretch within 5 units of 450.
3. On the vertical axis, click the red triangle next to Sulfur and select Silane.
Figure 12.8 Contour Profiler for Bounce Data.jmp
The plot shows the contour of values of Silane and Silica for Stretch at 425 and Sulfur at 2.3.
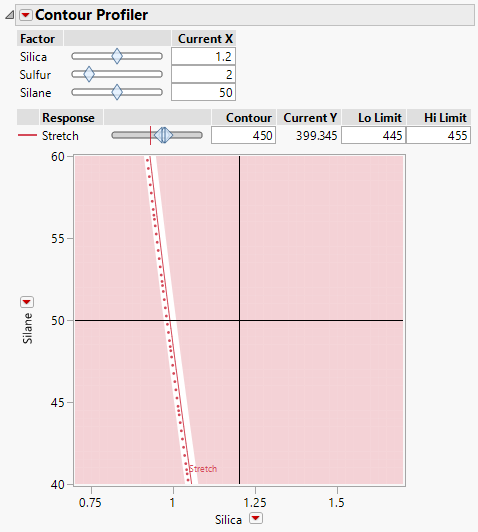
4. Set the Current X for Sulfur to 2.
5. Set the Contour for Stretch to 450.
6. Set the Lo Limit and Hi Limit for Stretch to 445 and 455, respectively. Press Enter.
Figure 12.9 Contour Profiler Showing Optimal Settings for Silica and Silane
The unshaded band of Silica and Silane values gives predicted Stretch between 445 and 455 when Sulfur is set at 2.0. The values on the solid red curve give predicted Stretch of 450.
7. Drag the crosshairs that appear in the plot to the unshaded band to find settings for Silica and Silane that are best for your process from a practical perspective.
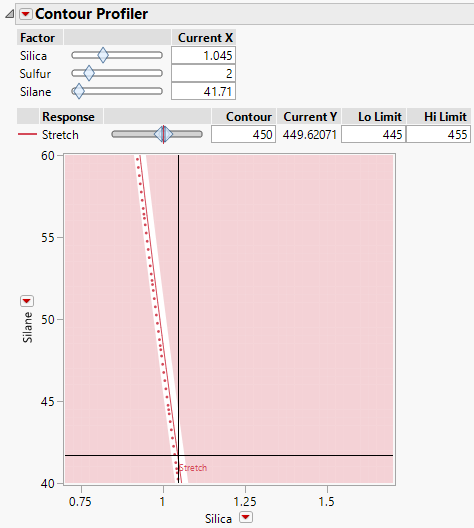
Suppose that your process is known to be more robust at low levels of Silane than at high levels. Then you might consider the settings in Figure 12.10.
Figure 12.10 Contour Profiler Showing Specific Settings for Silica and Silane
For Sulfur = 2.0, the factor settings identified by the crosshairs are Silica = 1.045 and Silane = 41.71. These settings are shown under Current X. At these settings, the predicted Stretch is 449.62071, shown next to Current Y.
For more information about the Contour Profiler, see Contour Profiler in Profilers.