モデル効果の構成
モデルの効果を指定するには、「モデルのあてはめ」起動ウィンドウの「モデル効果の構成」を用います。指定できるモデルの例については、「モデルの指定」のテンプレートを参照してください。
追加
[追加]ボタンをクリックすると、選択されている列がモデルに効果として追加されます。モデルに効果を追加するには、「列の選択」リストで選択してから、[追加]ボタンをクリックするか、[マクロ]ボタンをクリックします。なお、交互作用や枝分かれ効果を指定するには、[交差]や[枝分かれ]を使います。また、追加された効果の属性は、[属性]の赤い三角ボタンで変更できます。追加された効果が計算においてどのように扱われるかは、変数の尺度や属性によって決まります。
メモ: 「モデル効果の構成」リストから効果を削除するには、効果をダブルクリックするか、効果を選択してから[削除]ボタン、Backspaceキー、またはDeleteキーを押します。
交差
[交差]ボタンをクリックすると、交互作用や多項式の効果が作成されます。「列の選択」リストで2つ以上の列を選択し、[交差]ボタンをクリックしてください。または、「列の選択」リストで1つ以上の変数を選択すると一緒に「モデル効果の構成」リストで1つ以上の効果を選択し、[交差]をクリックしてください。
交互作用の効果が、JMPにおいてどのようにパラメータ化されるかについては、統計的詳細を参照してください。
メモ: 「交差」および「枝分かれ」において組み合わせることができる列は、最大10列です。
交互作用の例
製品のコーティングに、ある染料を利用する例を考えてみましょう。染料のpHと色素濃度が、コーティングの最終的な色に影響しています。そこで、pHが高いときと低いとき、色素濃度の濃いときと薄いときで組み合わせた実験を行いました。染料のpHが最終的な色に与える影響は、色素濃度が高いときよりも、低いときの方が大きいです。このような状態が、交互作用です。この例の交互作用をJMPで指定するには、「モデル効果の構成」リストに、「pH * 色素濃度」という交互作用項を含めます。これで、交互作用の項がモデルに含められます。
枝分かれ
[枝分かれ]ボタンをクリックすると、枝分かれ効果が作成されます。ある効果(B)の各水準が別の効果(A)における特定の1水準に含まれている場合、「BはAから枝分かれしている」といいます。これは通常、B[A](「Aから枝分かれしているB」と読む)と表記されます。枝分かれでは、効果が階層型になっています。Aは外側効果、Bは内側効果と呼ばれます。枝分かれの項はカテゴリカルでなければなりません。
メモ: 枝分かれの項は、外側効果から先に指定する必要があります。たとえば、BがAから枝分かれしていて、CがBから枝分かれしている場合は、モデルをA、B[A]、C[B,A](または、A、B[A]、C[A,B])と指定します。「交差」および「枝分かれ」において組み合わせることができる列は、最大10列です。
枝分かれ効果の例
枝分かれ効果を理解するために、ここでは、ある2つの中学校の数学クラスに関する例を挙げます。一方の中学校には数学教師が3名おり、他方の中学校には2名います。そして、各教師たちは、それぞれ幾つかのクラスを教えています(これらのクラスの生徒は重複していません)。この例では、学校(A)から教師(B)が枝分かれしており、さらに、教師(B)からクラス(C)が枝分かれしています。これらの効果は、「モデルのあてはめ」起動ウィンドウで次のように指定します。
1. AとBの両方を「モデル効果の構成」パネルに追加します。
2. 「モデル効果の構成」パネルで、Bを選択します。
3. 「列の選択」リストで、Aを選択します。
4. [枝分かれ]ボタンをクリックします。これにより、Bが効果B[A]に変換されます。
5. 「モデル効果の構成」パネルにCを追加します。
6. 「モデル効果の構成」パネルで、Cを選択します。
7. 「列の選択」リストで、AとBを選択します。
8. [枝分かれ]ボタンをクリックします。これにより、Cが効果C[A, B]に変換されます。
マクロ
「マクロ」リストには、一般的によく使われる効果が用意されています。この[マクロ]機能を用いることにより、「モデル効果の構成」リストに効果を入力する手間を省けます。
完全実施要因
「列の選択」リストで選択された列に対し、すべての主効果と交互作用を作成します。入力される順序は、「列の選択」リストでの主効果の順序に基づきます。別の順序で入力したい場合は、後述の「すべての組み合わせ」を参照してください。
設定された次数まで
すべての主効果と、指定した次数までの交互作用を作成します。次数は[マクロ]ボタンの下の「次数」ボックスで指定します。
すべての組み合わせ
[完全実施要因]オプションと同じ効果を作成しますが、効果は次数の順にリストされます。最初に主効果、次に2次の交互作用、その次に3次の交互作用という順でリストされます。
応答曲面
主効果、2次の交互作用、2乗項を作成します。このとき、主効果には「応答曲面」の属性が割り当てられます。主効果に応答曲面の属性を適用し、[標準最小2乗]の手法を選択した場合、「応答曲面」レポートが表示されます。このレポートには、最適解と応答曲面の形状に関する情報が表示されます。
メモ: このオプションは、カテゴリカルな効果に対して2乗項を作成しません。
属性の「応答曲面効果」と、『実験計画(DOE)』の応答曲面計画も参照してください。
配合応答曲面
主効果と2次の交互作用を作成します。このとき、主効果には「応答曲面」と「配合」の属性が割り当てられます。[標準最小2乗]の手法では、「配合」の属性が割り当てられている場合、配合モデルがあてはめられます。また、「配合」属性とともに、「応答曲面」属性も割り当てられていると、配合効果の応答曲面モデルがあてはめられ、「応答曲面」レポートが作成されます。
属性の「配合効果」と、『実験計画(DOE)』の応答曲面計画も参照してください。
多項式の次数
主効果と、指定した次数までの多項式の項を作成します。次数は[マクロ]ボタンの下の「次数」ボックスで指定します。
メモ: このオプションは、カテゴリカルな効果に対して多項式の項を作成しません。
Schefféの3次多項式
主効果と特定の交互作用から構成された、Schefféの3次多項式を作成します。これらの項によって構成されるモデルは、配合計画における3次多項式の応答曲面モデルになっています。
配合実験データに3次多項式モデルをあてはめる場合、X1*X1*X2といった偶数乗の項は推定できません。そこで、Schefféの3次多項式モデルでは、代わりに、X1*X2*(X1 – X2)という形式の項を使います。
Schefféの3次多項式の項は、「次数」ボックスに3と入力し、[マクロ]から[配合応答曲面]コマンドを選択して含めることもできます。
部分 3次
主効果、2次の交互作用、2乗項、および、主効果と2乗項の交互作用を作成します。このマクロは、「応答曲面」のマクロで定義された項に、主効果と2乗項の交互作用を追加したものです。
メモ: このオプションは、カテゴリカルな効果に対して2乗項を作成しません。
 連続変数の複合化
連続変数の複合化
複数の連続尺度の列を1つの効果にまとめてレポートします。レポートの「効果の要約」において、ここで複合化した効果をまとめて追加、削除することができます。また、複合化された効果について、まとめててこ比プロットを描いたり、検定を行ったりします。この機能は、元データがダミー変数で構成されている場合に役立ちます。
メモ: 連続尺度ではない列は、[連続変数の複合化]に指定することはできません。
属性
「属性」リストによって、「モデル効果の構成」リストで選択されている効果に属性を割り当てることができます。
変量効果
効果に変量効果の属性を割り当てます。変量効果の詳細については、変量効果と推定方法の指定を参照してください。
応答曲面効果
効果に「応答曲面」の属性を割り当てます。この属性を用いるときには、関連する2乗項や2次交互作用などが、「モデル効果の構成」リストに含まれていなければなりません。「マクロ」リストの[応答曲面]オプションを使用すると、自動的にこれらの項が生成され、主効果に応答曲面の属性が割り当てられます。なお、交互作用や多項式の項には「応答曲面」の属性を割り当てる必要はありません。主効果だけに、この属性を割り当ててください。
対数分散効果
効果に対数分散の属性を割り当てます。この属性が指定された効果は、分散に対するモデル式に含まれます。
平均と分散の両方に関してモデルに含めたい効果は、2回指定する必要があります。平均と分散の両方に同じ効果を含めたい場合には、まずその効果に[対数分散効果]属性を与えて、その後、もう一度、同じ効果をモデルに追加します。または、タブ形式の場合には、[平均の効果]と[分散の効果]の両方のタブに入力することでも指定できます。
配合効果
主効果に配合の属性を割り当てます。これは、配合に関係する主効果を指定するのに使用されます。なお、[マクロ]リストの[配合応答曲面]オプションは、選択した効果に自動的に配合属性を割り当て、可能な場合は「応答曲面」レポートを表示します。
除外した効果
効果に除外の属性を割り当てます。指定された効果は、モデルの推定には使われません。ただし、あてはまりの悪さの検定においてデータをグループ化する際には、ここで除外した効果も使用されます。また、[標準最小2乗]手法では、除外した効果に対しても、最小2乗平均の表が作成されます。
節点スプライン効果
連続尺度の主効果に節点スプラインの属性を割り当てます。これにより、3次の節点スプラインがあてはめられます。節点スプライン効果を参照してください。
節点スプライン効果
節点スプラインを使うと、滑らかな関数をあてはめることができます。ある説明変数Xに節点スプライン効果を割り当てたとしましょう。その場合、この1つの説明変数Xにk個の節点が設定され、k - 2個の効果がモデルに追加されます。これらの効果により、モデルが区分3次多項式によって表される節点スプラインとなります。各区分は、節点によって分割されます。節点スプラインについては、Stone and Koo(1985)を参照してください。
節点スプラインにおける区分の数は、ユーザが指定する節点の個数によって決まります。節点スプラインの係数を推定する方法は、各手法で異なります。
節点の配置方法は、Stone and Koo(1985)に従っています。データ点が100個以下の場合は、最小と最大から5番目の点が、それぞれ最初と最後の節点になります。データ点が101個以上の場合は、節点が5つ以下のときは5%と95%の分位点が最初と最後の節点になり、節点が6つ以上のときは2.5%と97.5%の分位点が最初と最後の節点になります。デフォルトの節点の数は、データ点が31以上の場合は5点、データ点が30以下の場合は3点です。
メモ: 節点スプライン曲線の効果は、連続尺度の主効果にしか設定できません。
変換
[変換]オプションは、「モデル効果の構成」で選択されているY列または主効果を変換します。
メモ: 「列の選択」リストで列を右クリックして[変換]を選ぶことでも、列を変換できます。列を右クリックして[変換]を選ぶと、「列の選択」リストに変換した列が表示されます。この変換した列は、「モデルのあてはめ」ウィンドウにおいて、データテーブルの列と同じ様に使用できます。『JMPの使用法』のJMPプラットフォームでの列の変換を参照してください。
なし
現在適用されている変換を削除します。
対数
選択された変数に、自然対数変換を適用します。
平方根
選択された変数に、平方根変換を適用します。
2乗
選択された変数に、平方変換を適用します。
逆数
変数Xを、逆数1/Xに変換します。
指数
選択された変数に、指数変換を適用します。
Arrhenius
変数T(摂氏での温度)にArrhenius変換を適用します。
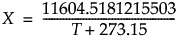
この変換は、Arrhenius式において、活性化エネルギーに乗じられる項です。
Arrhenius逆変換
変数XにArrheniusの逆変換を適用します。
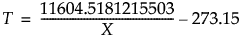
ロジット
選択された変数を、ロジット変換します(選択された変数pは、0より大きく、1未満でなければいけません)。ロジット変換は、ロジスティック変換の逆変換です。
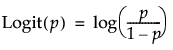
ロジスティック
選択された変数を、ロジスティック変換します(変換された結果は、0より大きく、1未満になります)。ロジスティック関数は、「シグモイド関数」や「ロジスト関数」などとも呼ばれています。
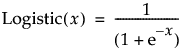
ロジットパーセント
選択された変数を、パーセントを単位としてロジット変換します(選択された変数pctは、0より大きく、100未満でなければいけません)。
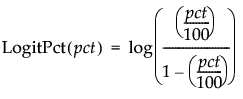
ロジスティックパーセント
選択された変数を、パーセントを単位としてロジスティック変換します(変換された結果は、0より大きく、100未満になります)。
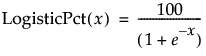
切片なし
切片項のないモデルをあてはめたい場合は、[切片なし]を選択してください。また、モデルのなかには、配合モデルのように、切片が構造上、必要ではないものがあります。そのような場合は、デフォルトで[切片なし]がオンになります。
「モデル効果の構成」のタブ
以下の手法では、タブを使ってもモデル効果を指定できます。
メモ: 最初の起動ダイアログで、効果に何らかの属性を適用すると、適用された属性によって効果の扱われ方が決まります。また、モデルを実行した後、レポートの赤い三角ボタンメニューから[モデルダイアログ]を選択すると、それらの効果が適切なタブに表示されます。
標準最小2乗
この手法では、次のような効果を指定できます。
[固定効果]タブ
固定効果を指定します。固定効果では、因子のそれぞれの水準が推定対象となります。水準ごとの平均を比較するのが主な目的です。
[変量効果]タブ
変量効果として扱う効果を指定します。変量効果における各水準は、母集団から無作為抽出された標本と見なされます。変量効果によって、応答がどれだけばらつくかを推定するのが主な目的です。
混合モデル
この手法では、次のような効果を指定できます。
[固定効果]タブ
固定効果を指定します。前述の「標準最小2乗」での説明を参照してください。
[変量効果]タブ
変量効果を指定します。このタブにおいて、分散成分モデルやランダム係数モデルを指定できます。
[反復構造]タブ
反復測定モデルにおける共分散構造を選択します。
対数線形-分散
この手法では、次のような効果を指定できます。
[平均の効果]タブ
平均をモデル化するのに用いる効果を指定します。
[分散の効果]タブ
分散をモデル化するのに用いる効果を指定します。
平均のモデル化にも、分散のモデル化にも用いたい効果は、両方のタブに入力してください。
生存時間(パラメトリック)
この手法では、次のような効果を指定できます。
[位置の効果]タブ
(対数変換した後の分布において)位置パラメータに対する効果を指定します。なお、この効果は、対数変換しない元の分布(たとえばWeibull分布)では、尺度パラメータへの効果に該当します。
[尺度の効果]タブ
(対数変換した後の分布において)尺度パラメータに対する効果を指定します。