バギングを使用して予測精度を測る例
バギングを使用して予測精度を測る例
バギングのもう1つの使用例は、標準誤差などの分布情報に基づいて、予測の精度を測ることです。[各予測を計算式として保存]オプションをバギングで使用できるプラットフォームでは、新しく追加されたデータに対して予測値を求め、その予測精度を検討することができます。[各予測を計算式として保存]オプションは、「標準最小2乗」・「一般化回帰」・「一般化線形モデル」の各プラットフォームにおけるバギングで使用できます。
「Tiretread.jmp」データテーブルで、「摩擦」のみを3因子で予測するとしましょう。この例では、「摩擦」を予測するために、一般化回帰モデルをあてはめます。次に、このモデルでバギングを実行します。最後に、新しく追加されたデータに対して予測値を求め、その予測の精度を検討します。検討材料として、予測の信頼区間を求めます。
一般化回帰モデルのあてはめ
1. [ヘルプ]>[サンプルデータフォルダ]を選択し、「Tiretread.jmp」を開きます。
2. [分析]>[モデルのあてはめ]を選択します。
3. 「摩擦」を選択し、[Y]をクリックします。
4. 「手法」のリストから[一般化回帰]を選択します。
5. 「シリカ」、「シラン」、「硫黄」を選択し、[マクロ]>[完全実施要因]をクリックします。
これにより、交互作用を含むすべての項がモデルに追加されます。
6. [実行]をクリックします。
7. [実行]をクリックします。
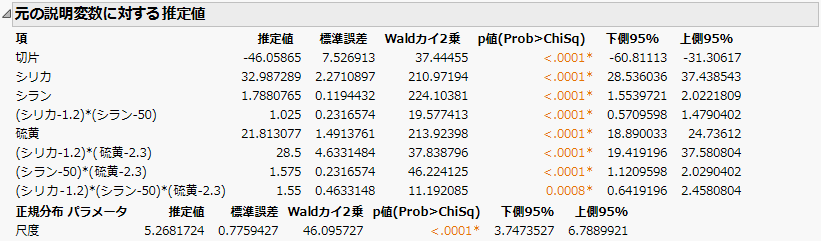
図3.35 「一般化回帰」レポートのパラメータ推定値
バギングの実行
1. 「Lasso (検証法: AICc, 分布: 正規)」の赤い三角ボタンをクリックし、[プロファイル]>[プロファイル]を選択します。
レポートの末尾に「予測プロファイル」が表示されます。
2. 「予測プロファイル」の赤い三角ボタンをクリックし、[バギング予測の保存]を選択します。
3. 「ブートストラップ標本数」の横に「500」と入力します。
4. (オプション)「乱数シード値」に「4321」と入力します。
メモ: 無作為に復元抽出されるため、結果はいつも同じではありません。以下と同じ結果を再現するには、上記の「乱数シード値」を設定してください。
5. [各予測を計算式として保存]が選択されていることを確認します。
6. [OK]をクリックします。
メモ: この設定では、バギングを使用して予測精度を高める例よりも処理に時間がかかる可能性があります。標本数が大きいほうが、予測分布の推定が向上します。
データテーブルのウィンドウに戻ります。応答変数ごとに、「予測式 <列名> バギング平均」、「<列名> ブートストラップ標準誤差」、「標準誤差 <列名> バギング平均」の3つの新しい列が追加されています。「予測式 摩擦 バギング平均」列が、最終的な予測値です。
新しく追加したデータに対する予測
データテーブルの各行に、「摩擦」の予測式とその標準誤差が追加されました。ここで、「シリカ」・「シラン」・「硫黄」がそれぞれ0.9, 43, 2という値になっているときの予測値を求めるとします。先ほど、[各予測を計算式として保存]オプションを使って、個々のバギングモデルの計算式を保存しました。この保存した計算式によって、応答変数である「摩擦」を予測し、その信頼区間を求めることができます。ここでは、先ほど述べた因子値について、M個の予測値を求め、その分布を求めることにします。これらM個の予測値を平均したものが、最終的な予測値となります。また、M個の予測値の分布を見れば、予測の精度がわかります。
1. データテーブルで、[行]>[行の追加]を選択します。
2. 「追加する行数」に「1」と入力し、[OK]をクリックします。
3. 新しい行の「シリカ」の列に、「0.9」と入力します。
4. 新しい行の「シラン」の列に、「43」と入力します。
5. 新しい行の「硫黄」の列に、「2」と入力します。
新しい行のすべての予測式の列が自動的に計算されます。
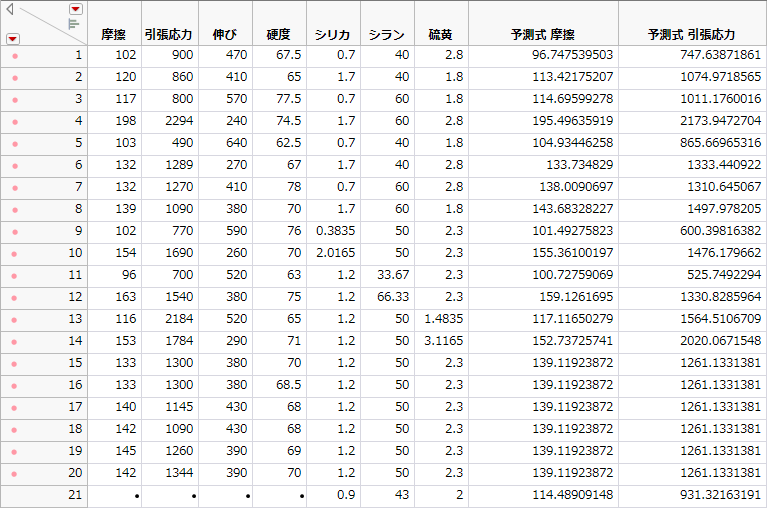
図3.36 新しい行の値
6. [テーブル]>[転置]を選びます。
7. 「バギング 摩擦 (500/0)」を選択し、[転置する列]をクリックします。
8. [OK]をクリックします。
9. [分析]>[一変量の分布]を選択します。
10. 「行 21」を選択して、[Y, 列]をクリックします。
メモ: 「行 21」は、新しく追加したデータ行の予測値に対応しています。
11. [OK]をクリックします。
12. 「行 21」の赤い三角ボタンをクリックし、[表示オプション]>[横に並べる]を選択します。
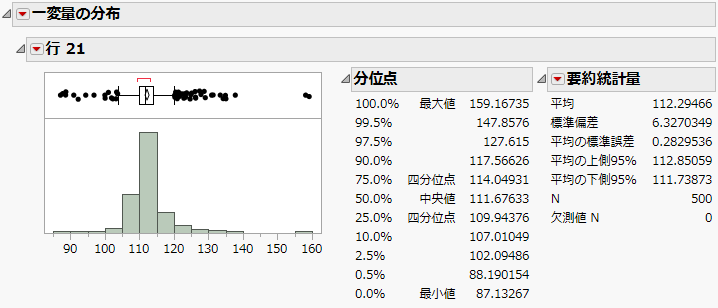
図3.37 「一変量の分布」レポート
Figure 3.37の「一変量の分布」レポートには、各バギングモデルからの摩擦の予測値の分布情報が表示されています。新しく追加したデータに対する「摩擦」の最終的な予測値は112.3です。これは、M個のバギング予測の平均値です。この予測値の標準誤差は、6.33です。分位点から、この新しく追加したデータに対する予測値の信頼区間も求めることもできます。この例では、新しい予測値の95%信頼区間は、102.09~127.62です。