Gauss過程

空間的モデルによるデータの補間や平滑化

「Gauss過程」プラットフォームは、複数の説明変数と1つの連続尺度の応答変数との関係をモデル化します。Gauss過程モデル（Gaussian process model）は、有限要素法のようなコンピュータによるシミュレーション実験などの分野で、データを完璧に補間するモデルとして広く利用されています。Gauss過程モデルは、確率的な誤差を持たないモデル、つまり入力変数（説明変数）の値が同じであれば必ず出力変数（応答変数）の値も同じであるようなデータを扱います。

「Gauss過程」プラットフォームは、データに対して空間相関モデル（spatial correlation model）をあてはめます。このモデルにおいては、2つのデータ行の間において、説明変数の値から計算される距離が長いほど、応答変数の相関が弱くなります。

このプラットフォームの目的の1つは予測式を求め、さらなる分析や最適化に役立てることです。

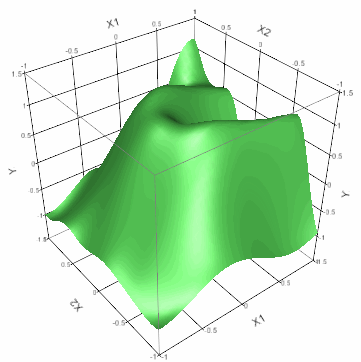
図17.1 Gauss過程の予測曲面の例 

目次

「Gauss過程」プラットフォームの例

「Gauss過程」プラットフォームの起動

「Gauss過程モデル」レポート

予測値と実測値のプロット

モデルのレポート

周辺モデルプロット

「Gauss過程」プラットフォームのオプション

「Gauss過程」プラットフォームの別例

Gauss過程モデルの例

カテゴリカルな説明変数を使ったGauss過程モデルの例

「Gauss過程」プラットフォームの統計的詳細

連続尺度の説明変数を使ったモデルの統計的詳細

カテゴリカルな説明変数を使ったモデルの統計的詳細

分散計算式のパラメータ化の統計的詳細

モデルのあてはめの統計的詳細