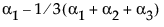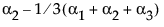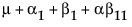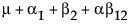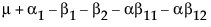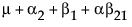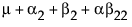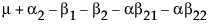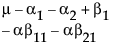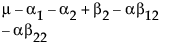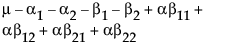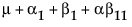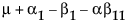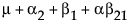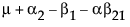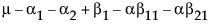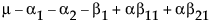名义型因子

在“拟合模型”平台中，对于设计矩阵，名义型因子变换为指标变量。SAS GLM 为每个名义型水平构造一个指示符列。JMP 为每个名义型水平构造相同的指示符列，但不包括最后一个水平。最后一个名义型水平出现时，从因子的所有其他列减去 1。例如，考虑针对 GLM 和 JMP 进行编码具有三个水平的名义型因子 A，如下所示。

在 GLM 中，线性模型设计矩阵具有列之间的线性相依性，最小二乘法解使用广义逆。选择的解发生在 A3 参数设置为零时。

在 JMP 中，将线性模型设计矩阵编码以便它达到满秩，除非存在缺失单元格或其他偶然的共线性。A 效应最后一个水平的参数是其他水平对应参数之和的负数，这使得在所有效应水平上参数之和为零。

参数的解释

注意：名义型水平的参数解释为该水平的预测响应与所有水平上的平均预测响应之间的差值。

一个因子水平的设计列构造为该因子水平的 0-1 指示符减去最后一个水平的指示符。这是得到上述参数解释的编码。

交互作用和交叉效应

GLM 和 JMP 均通过计算要交叉的因子的设计列所在行的直积来构造交互作用效应。例如，GLM 代码

PROC GLM;

	CLASS A B;

	MODEL A B A*B;

生成以下设计矩阵：

使用 JMP 拟合模型命令并请求列 A 和 B 的析因模型将得到以下设计矩阵。请注意该矩阵中的 A13 是上一矩阵中的 A1–A3。但是，当前矩阵中 A13B13 是 A13*B13。

当问题涉及具有少数几个水平的因子的交互作用时，JMP 编码可以节省内存和一些计算时间。

依据 3*3 交叉模型的参数，单元格的期望值为：

嵌套效应

GLM 中的嵌套效应采用与交互作用效应相同的编码方式，因为 GLM 通过不在模型中的项确定正确的检验。不包括在模型中的任何效应可通过包含的交互作用（或等价的嵌套）效应来吸收。

在 JMP 中嵌套效应的编码方式有所不同。JMP 使用括号里的项作为每个组的分组项。对于嵌套项的每个水平组合，JMP 在括号外构造效应。外部项的水平不需要在嵌套项的水平上排列。构造设计列和参数时单独处理嵌套的每个水平。

名义型因子的最小二乘均值

在将所有其他因子设置为某个中性值后，最小二乘均值是对应于某个水平组合的预测值。直接连续回归变量的中性值定义为样本均值。具有未涉及的名义型因子的效应的中性值定义为水平上所取的平均效应（它导致我们的编码中全部为零）。在有序型最小二乘均值中，有序型因子使用另一中性值。最小二乘均值可能无法估计，若无法估计，将它们标记为无法估计。在不使用权重的情况下，JMP 中的最小二乘均值与 SAS PROC GLM (Goodnight and Harvey 1978) 中的最小二乘均值一致。使用权重变量时，JMP 对中性值使用加权均值而 SAS PROC GLM 使用未加权均值。

有效假设检验

通常，JMP 生成的假设检验与大多数其他可信程序（如 SAS PROC GLM，它使用假设类型 III 和 IV）的假设检验是一致的。以下两节说明它们的区别。

在 SAS PROC GLM 中，通过查看一般形式的可估计函数并找到仅涉及关注的效应和关注效应包含的效应的函数，以构造 III 和 IV 类假设检验 (Goodnight 1978)。

在 JMP 中构造相同的检验。但是因为参数化方式不同，可以通过对某效应的所有参数执行联合检验来检验该效应（假定现在为满秩）。检验不涉及包含交互作用参数，因为编码已使它们不涉及对包含的效应的检验。

若有缺失单元格或其他奇异性，JMP 检验与 GLM 检验不同。有几种描述它们的方式：

• JMP 检验等价于检验最小二乘均值存在差异，至少对于主效应是这样。若无法估计最小二乘均值，则检验不能包括一些比较，因此会损失自由度。对于交互作用，JMP 检验最小二乘均值差异是否刚好超过模型中所包含效应描述的边缘模式。

• JMP 通过以下方式检验效应：比较具有该效应的模型的 SSE 和没有该效应的模型的 SSE。JMP 参数化模型以使该方法变得有意义。

• JMP 实现有效假设检验（如 Hocking (1985, pp. 80–89, 163–166) 中所述），尽管 JMP 使用结构参数化而非单元格均值参数化。有效假设检验从效应所需的假设开始检验，并包括该检验的“尽量多的内容”。当然，若存在具有缺失单元格的包含效应，该检验必须去掉部分假设，因为完整的假设将是无法估计的。有效假设是从完整假设中删除尽量少的内容得来的。

• JMP 和 GLM（以及其他程序）中与是否存在缺失单元格有关的假设检验的差异不再被视为关注的检验。若交互作用是显著的，则不需要执行被包含的主效应的检验。若交互作用不是显著的，则随时可以从模型中删除它。一些检验甚至不是唯一的。若您重新标记缺失单元格设计中的水平，GLM IV 类检验会发生变化。

下一节详细说明该主题。

名义型效应中的奇异性和缺失单元格

考虑设计列中存在线性相依性的情况。使用 JMP 编码时，这种情况不会发生，除非没有足够的数据来填充需要估计的组合，或除非存在效应的某种混杂或共线性。

存在线性相依性时，参数的最小二乘解可能不是唯一的，无法执行一些假设检验。当发现参数的设计列与模型中前面的效应是线性相依时，JMP选择的策略是按顺序将参数估计值设置为零。报表中的特殊列显示哪些参数估计值清零以及可以估计哪些参数估计值。单独的奇异性报表显示存在哪些线性相依性。

若存在奇异性，JMP 所检验的假设会不同于 GLM 选择的假设。与 GLM 相比，通常 JMP 找到更少的自由度进行检验，因为它将检验保持为更高的边缘标准。换句话说，JMP 检验始终对应于该效应的最小二乘均值的检验，但是 GLM 检验有时并不具有该特性。

例如，考虑具有交互作用和一个缺失单元格的双因子模型，其中 A 有三个水平，B 有两个水平，A3B2 单元格缺失。

每个单元格的期望值为：

显然，具有数据的任何单元格具有可估计的期望值。缺失的单元格具有无法估计的期望值。实际上，单元格的期望值恰好是奇异性报表中的设计列的以下线性组合

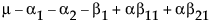
假定您要构造比较 B1 和 B2 的最小二乘均值的检验。在本例中，上表中的行平均值给出这些最小二乘均值。

LSM(B1) =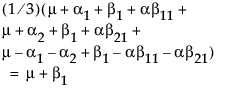

LSM(B2) =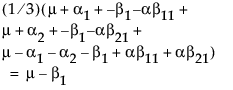

LSM(B1) – LSM(B2) =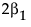

请注意，这说明针对 b1 参数的检验等价于检验最小二乘均值是相同的。但是因为 b1 无法估计，该检验无法进行，这意味着没有用于它的自由度。

现在，构造 A 水平上的最小二乘均值检验。

LSM(A1) =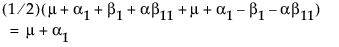

LSM(A2) =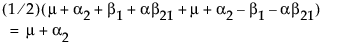

LSM(A3) =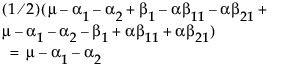

LSM(A1) – LSM(A3) =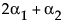

LSM(A2) – LSM(A3) =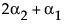

这些都是无法估计的，但是有另一个可以估计的比较，即比较没有缺失单元格的两个 A 列。

LSM(A1) – LSM(A2) =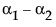

该组合确实由 JMP 检验的（使用自由度为 1 的检验），尽管在效应中有两个参数。

通过计算奇异性组合的内积并检查它是否为零，可以验证可估性：

结果是任意交互作用的缺失单元格的设计列始终剔除主效应的自由度（对于名义型因子）。因此，最小二乘均值的不可估性和检验对应于这些最小二乘均值的效应的自由度损失之间有直接关系。

这如何与 GLM 所做的进行比较？当没有缺失单元格时，GLM 和 JMP 执行相同的检验。即，它们有效地检验最小二乘均值是相等的。但是当 GLM 遇到奇异性时，它以不同方式不再关注这些单元格，具体取决于它们属于类型 III 还是类型 IV。对于类型 IV，它查找可以找到的可估计组合。这些组合可能不是唯一的，若您重新排序水平，可能得到不同的结果。对于类型 III，它执行可估计函数的一些正交化来获得唯一检验。但是，根据单元格均值，检验可能不是很好解释的。

JMP 方法具有几个优点，尽管起初它与使用 GLM 相比可能损失更多自由度：

1. 这些检验在原理上与 LSM 关联。

2. 这些检验在计算上很简单，使用重新参数化的模型的简化平方和。

3. 这些检验与 Hocking 的“有效假设检验”一致。

4. 这些检验是整体边缘检验，即它们始终完全涵盖交互作用中的其他效应。

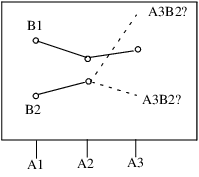
最后一点需要更详尽阐述：我们来看上一示例（A3B2 具有缺失单元格）中单元格均值的期望值图。

图 A.1 单元格均值的期望值 

该图显示具有缺失单元格的期望单元格均值。在 B 水平上刻画 A1 和 A2 单元格的均值。JMP 方法指示您不能检验具有缺失 A3B2 单元格的 B 主效应，因为缺失单元格的均值可能是交互作用项允许的任何值。若缺失单元格的均值是显示的更高值，B 效应可能是检验显著的。若它是更低的值，则可能是检验不显著的。该点是您不知道的点。它是声明最小二乘均值不可估计时它们要表达的内容。它也是效应的假设所说的那样—您不知道。

若您要检验涉及单元格子集的边缘的假设，则这是 GLM 类型 IV 要做的事。在 JMP 中，您必须通过使用很多计算分割效应或使用对比来自行构造这些检验。

JMP 和 GLM 假设

有缺失单元格时，GLM 工作方式不同于 JMP，它生成不同的假设检验。特别是，GLM 无法识别效应中嵌套和交叉的任何差异，但是 JMP 可以识别。假定您进行嵌套设计时，具有带不同水平数的三层嵌套：A、B(A) 和 C(A B)。

图 A.10 显示采用 GLM 参数的主效应 A 的检验。第一个列集是 JMP 执行的检验。第二个列集是 GLM 类型 IV 执行的检验。第三个列集等价于 JMP 执行的检验，它是前两列与以下矩阵相乘得到的：

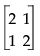
它可与 GLM 检验进行比较。最后一个列集是 GLM 类型 III 检验。区别是检验在包含效应上的分布不同。在 JMP 中，它似乎更倾向于自上而下分层。在 GLM 类型 IV 中，检验似乎更倾向于由下而上。实际上，检验统计量通常是相似的。

从 JMP 参数化的角度，A 的检验为：

因此，从 JMP 的角度看，GLM 检验有点奇怪，它对 a1b24 参数设置系数。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).