「主成分分析」レポートのオプション
主成分分析のタイトルバーにある赤い三角ボタンをクリックすると、次のようなオプションが表示されます。
メモ: 一部のオプションは、[横長データ]または次元数を指定した分散推定法では表示されません。
主成分分析
([横長データ]または次元数を指定した分散推定法では使用できません。)[相関係数行列から]・[共分散行列から]・[非尺度化・非中心化]のいずれかに基づいて主成分を求められます。
相関
([横長データ]または次元数を指定した分散推定法では使用できません。)相関係数行列の表示/非表示を切り替えます。
メモ: 相関係数行列の対角要素は1.0になっています。
共分散行列
([横長データ]または次元数を指定するアルゴリズムでは使用できません。)共分散行列の表示/非表示を切り替えます。
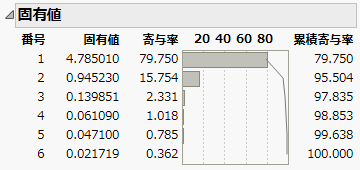
固有値
各主成分に対応する固有値が、大きい方から順に表示されます。固有値は、多変量データにおける分散の合計が各主成分によってどれぐらい説明されるかを表します。
固有値のスケールは、分析対象とする行列によって異なります。
– [相関係数行列から]オプションを選んだ場合の固有値は、相関係数行列に対する固有値となります。この固有値の合計は変数の個数に一致します。
– [共分散行列から]オプションを選んだ場合の固有値は、共分散行列に対する固有値となります。
– [非尺度化・非中心化]オプションを選んだ場合の固有値は、積和行列を標本サイズで割ったものの固有値です。
赤い三角ボタンのメニューから[Bartlettの検定]オプションを選択した場合、各固有値に対する仮説検定(Figure 4.6)が行われます(Jackson, 2003)。
図4.5 固有値
固有ベクトル
各主成分(左から順に第1主成分、第2主成分、と並ぶ)の固有ベクトルの表示/非表示を切り替えます。固有ベクトルを係数として計算された元の変数の線形結合が、主成分スコアです。各固有ベクトルはノルムが1になるように標準化されています。
メモ: 表示される固有ベクトルの個数は、相関係数行列のランクと同じか、または「疎」の推定法が選択されている場合は、起動ウィンドウで指定された成分の個数です。
Bartlettの検定
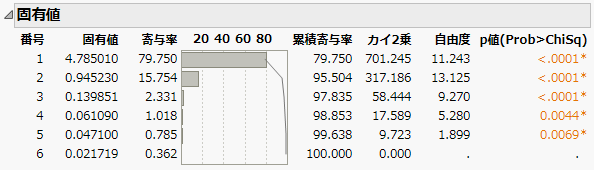
([横長データ]または次元数を指定するアルゴリズムでは使用できません。)固有値の等質性に対する検定結果の表示/非表示を切り替えます(「固有値」表に追加されます)。この検定では、複数の固有値が等しいかどうかに関する検定に対して、カイ2乗値・自由度(DF)・p値(prob > ChiSq)が計算されます。Bartlett(1937, 1954)を参照してください。
図4.6 Bartlettの検定
負荷量行列
各主成分の負荷量を示した表の表示/非表示を切り替えます。表中の数値の透明度は、負荷量の絶対値が、どれぐらいゼロに近いかを示しています。負荷量の絶対値がゼロに近いほど透明になります。このオプションは、各主成分の負荷量のプロットも表示します。ボタンを使って、横軸と縦軸を切り替えられます。「負荷量行列のプロット」の赤い三角ボタンのメニューには、以下のオプションがあります。
プロットの選択
主成分の負荷量の表示方法を指定します。[複数の次元]オプションでは、指定した個数の主成分すべてについて、負荷量が表示されます。[1次元ずつ]オプションでは、選択した1つの主成分の負荷量が表示されます。
棒のスタイル
棒を横に並べて表示するか、積み重ねて表示するかを設定できます。
追加変数として連続変数やカテゴリカル変数を指定した場合は、その座標の表も表示されます(カテゴリカル変数を指定した場合は、各水準の座標が表示されます)。追加変数として連続変数を指定した場合、追加変数の負荷量も、負荷量プロットに描かれます。
負荷量と座標がどのように尺度化されるかは、主成分分析の対象となった行列で異なります。
– [相関係数行列から]オプションを選んだ場合、i番目の負荷量の列は、i番目の固有ベクトルにi番目の固有値の平方根を掛けたものとなります。 i,j番目の負荷量は、i番目の変数とj番目の主成分との相関になっています。
– [共分散行列から]オプションを選んだ場合、第i列、第j行の負荷量は、i番目の固有ベクトルにi番目の固有値の平方根を掛けて、j番目の変数の標準偏差で割ったものとなります。i,j番目の負荷量は、i番目の変数とj番目の主成分との相関になっています。
– [非尺度化・非中心化]オプションを選んだ場合、第i列、第j行の負荷量は、i番目の固有ベクトルにi番目の固有値の平方根を掛けて、j番目の変数の平均積和で割ったものとなります。ここで言う「j番目の変数の平均積和」とは、積和行列(X′X/n)のj番目の対角要素を行数で割った値です。
メモ: 積和行列を分析対象とする場合、i,j番目の負荷量はi番目の変数とj番目の主成分の間の相関ではありません。
濃淡表示の負荷量行列
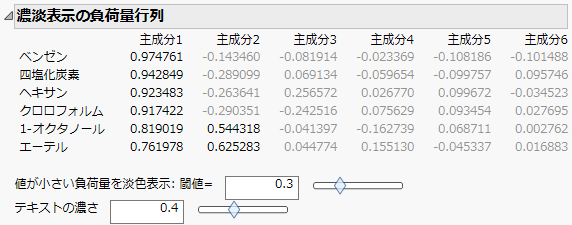
各主成分の負荷量を示した表の表示/非表示を切り替えます。この表の変数は、第1主成分の負荷量によって降順に並べ替えられています。したがって、この負荷量の降順で変数が並べられることになります。
図4.7 濃淡表示の負荷量行列
値が小さい負荷量を淡色表示: 閾値=
「濃淡表示の負荷量行列」レポートで薄く表示する負荷量の閾値を指定します。テキストボックスかスライダーを使って、この閾値を変更できます。指定した閾値より小さい絶対値の負荷量が淡色表示になります。
テキストの濃さ
「濃淡表示の負荷量行列」レポートで淡色表示する値の透明度。テキストボックスかスライダーを使って、淡色表示する負荷量の透明度を変更できます。透明度は0~1です。低い値ほど透明度は高くなります。たとえば、透明度を0に設定すると、閾値以下の負荷量はまったく表示されなくなります。透明度を1に設定すると、すべての負荷量はそのまま表示されます。
変数の余弦2乗
各変数の余弦2乗を示した表の表示/非表示を切り替えます。追加変数を指定した場合は、それら追加変数の余弦2乗の表も表示されます。各変数の余弦2乗を主成分全体で合計したものは、1になります(100%になります)。ある変数の余弦2乗は、その変数が該当の主成分によってどれぐらい良く表されているかを示します。該当の変数を表すのにいくつの主成分が必要かを知る目安になります。このオプションを選ぶと、主成分の余弦2乗を描いたプロットも表示されます。ボタンを使って、横軸と縦軸を切り替えられます。「変数の余弦2乗プロット」の赤い三角ボタンのメニューには、以下のオプションがあります。
プロットの選択
主成分の余弦2乗の表示方法を指定します。[複数の次元]オプションでは、指定した個数の主成分すべてについて、余弦2乗が表示されます。[1次元ずつ]オプションでは、選択した1次元の主成分での余弦2乗が表示されます。
棒のスタイル
棒を横に並べて表示するか、積み重ねて表示するかを設定できます。
メモ: ただし、次元数を指定するアルゴリズムを使用し、選択した成分が2次元以下の場合、1次元もしくは2次元だけのプロットになります。
変数の偏寄与率
各変数の偏寄与率を示した表の表示/非表示を切り替えます。偏寄与率を見ると、各変数が各主成分に寄与する割合がわかります。このオプションを選ぶと、偏寄与率のプロットも表示されます。ボタンを使って、横軸と縦軸を切り替えられます。「変数の偏寄与率プロット」の赤い三角ボタンのメニューには、以下のオプションがあります。
プロットの選択
主成分の偏寄与率の表示方法を指定します。[複数の次元]オプションでは、指定した個数の主成分すべてについて、偏寄与率が表示されます。[1次元ずつ]オプションでは、選択した1次元の主成分での偏寄与率が表示されます。
棒のスタイル
棒を横に並べて表示するか、積み重ねて表示するかを設定できます。
メモ: ただし、次元数を指定するアルゴリズムを使用し、選択した成分が2次元以下の場合、1次元もしくは2次元だけのプロットになります。
要約プロット
デフォルトのレポートで作成された要約情報の表示/非表示を切り替えます。この要約情報には、固有値のプロット、主成分スコアのプロット、主成分負荷量のプロットが含まれます。デフォルトでは、レポートには最初の2次元に関する主成分のスコアプロットと負荷量プロットが表示されます。何次元目の主成分をプロットするかを変更することもできます。「主成分分析」レポートを参照してください。
メモ: データに欠測値が含まれる場合、補完したスコアがスコアプロットに表示されます。
ヒント: 負荷量プロットの矢印の先を選択すると、データテーブル内の対応する列が選択されます。Ctrlキーを押したまま矢印の先をクリックすると、列の選択を解除できます。
バイプロット
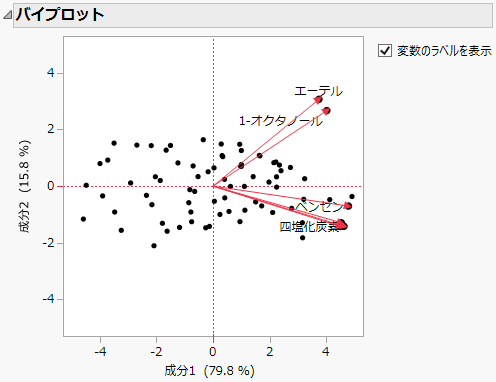
スコアと負荷量を重ねて描いたバイプロットの表示/非表示を切り替えます。指定した成分数に対するバイプロットが描かれます。
メモ: データに欠測値が含まれる場合、補完したスコアがバイプロットに表示されます。
図4.8 バイプロット
メモ: バイプロットでは、主成分スコアは点で、主成分負荷量は矢印で描かれています。
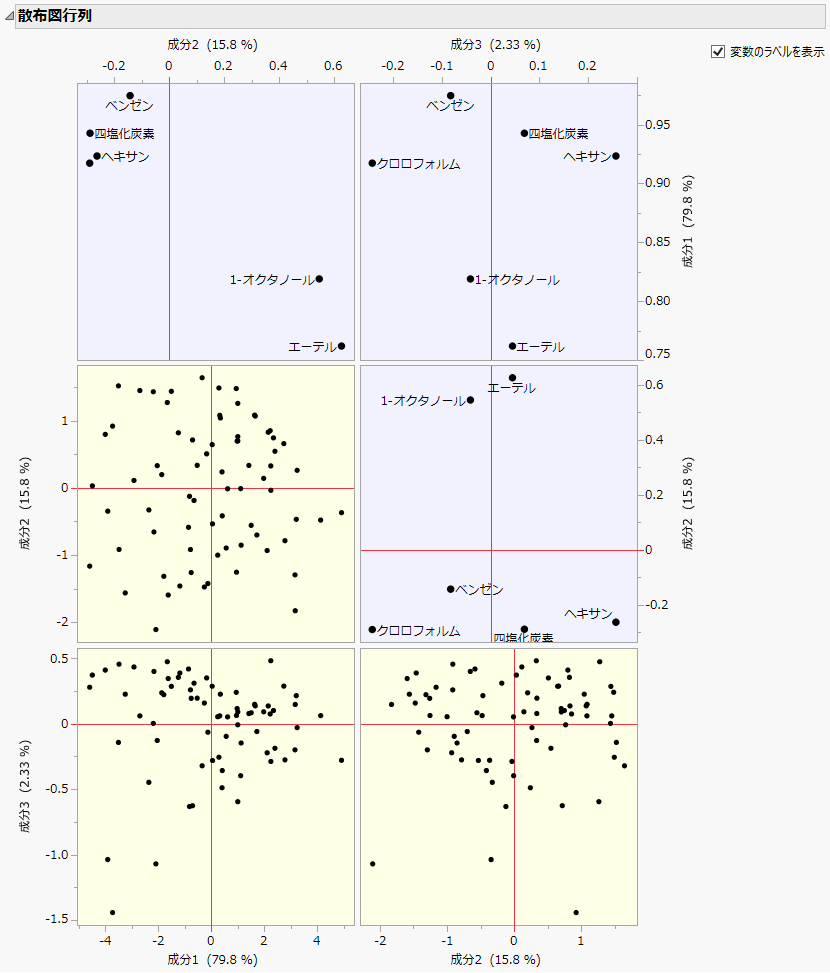
散布図行列
主成分スコアと主成分負荷量をプロットした散布図行列の表示/非表示を切り替えます。この散布図行列には、主成分スコアのプロットが左下に、主成分負荷量のプロットが右上に描かれています。主成分スコアのプロットの背景色は黄色、主成分負荷量のプロットの背景色は青色になっています。
メモ: データに欠測値が含まれる場合、補完したスコアが散布図行列に表示されます。
図4.9 散布図行列
メモ: 散布図行列に表示される負荷量プロット行列は、[負荷量プロット]オプションを選択したときに得られる負荷量プロット行列を転置したものです。
スクリープロット
各成分の固有値をプロットしたグラフの表示/非表示を切り替えます。このグラフは成分数に対して固有値をプロットしたもので、求める主成分の次元数を決めるのに役立ちます。
スコアプロット
主成分スコアをプロットした散布図行列の表示/非表示を切り替えます。指定した成分数に対する散布図が描かれます。Figure 4.4は主成分スコアをプロットした例です(一番左側のプロット)。
負荷量プロット
主成分負荷量のプロットの表示/非表示を切り替えます。指定した成分数に対するプロットが描かれます。負荷量プロットでは、変数が30個以下の場合は変数のラベルが表示されます。変数が30個より多い場合は、デフォルトでラベルが非表示になります。変数のラベルは、Figure 4.4(一番右側のプロット)では表示されています。
ヒント: 負荷量プロットの矢印の先を選択すると、データテーブル内の対応する列が選択されます。Ctrlキーを押したまま矢印の先をクリックすると、列の選択を解除できます。
補完したスコアプロット
([横長データ]または次元数を指定した分散推定法では使用できません。)欠測値をすべて補完したスコアプロットが作成されます。このオプションは、欠測値がある場合にのみ使用できます。
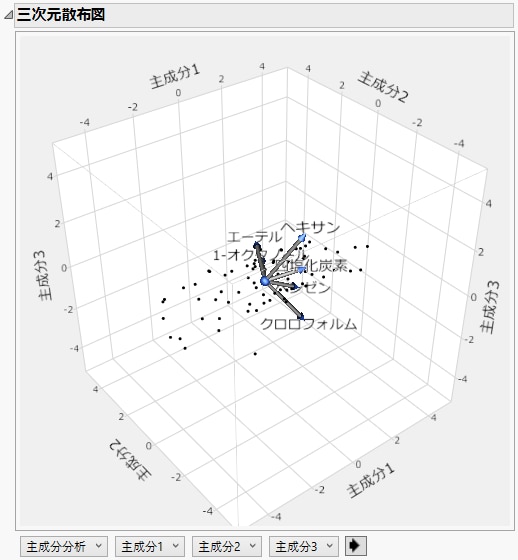
三次元スコアプロット
([横長データ]または次元数を指定するアルゴリズムでは使用できません。)主成分スコアの三次元散布図が表示されます。初期のプロットでは、最初の3つの主成分がプロットされています。
メモ: データに欠測値が含まれる場合、補完したスコアが三次元スコアプロットに表示されます。
図4.10 三次元スコアプロット
プロットのソース
どの値をプロットするかを選択します。使用できるオプションは、[主成分分析]・[回転後の主成分]・[データ列]です。
変数の指定
各軸にプロットする変数を指定します。[主成分分析]オプションまたは[回転後の主成分]オプションを選択した場合、主成分スコアがプロットされます。[データ列]オプションを選択すると、元の変数がプロットされます。
サイクルボタン![]()
軸にプロットする変数が順番に変更されます。
このプロットでは、変数が中心からの矢印で描かれます。この矢印は、バイプロット線といい、主成分の空間上に元の変数の向きを近似的に描いています。変数が2つまたは3つしかない場合、バイプロット線は、近似ではなく、元の変数の正確な向きを表します。これらのバイプロット線は、主成分負荷量を表しています。
スコアに対する楕円
主成分スコアの要約プロットにおいて、楕円の表示/非表示を切り替えます。楕円の種類には、累積確率に基づくものと、シグマの何倍になっているかに基づくものがあります。デフォルトでは、95%信頼楕円が表示されます。
楕円の大きさ
スコアに対する楕円の描き方を指定するサブメニューが含まれます。楕円内の累積確率か、または、kシグマを指定します。楕円内の累積確率pと、kシグマは、p = 1 - exp(-k2/2)という関係になっています。
表示オプション
矢印線
矢印を表示できるプロットにおいて、矢印の表示/非表示を切り替えることができます。変数の数が1000個以下の場合、矢印が表示されます。変数が1000個より多い場合は、デフォルトにおいて矢印は表示されません。
追加変数の表示
(追加変数を指定したときだけ使用できます)バイプロット・スコアプロット・負荷量プロットにおいて、連続尺度の追加変数を表す矢印、および、カテゴリカルな追加変数のマーカーの表示/非表示を切り替えます。
外れ値分析
「外れ値分析」レポートの表示/非表示を切り替えます。この分析により、T2や各行の寄与に関する統計量に基づき、外れ値を検出できます。外れ値分析を参照してください。
因子分析
([横長データ]または次元数を指定した分散推定法では使用できません。)回転を伴う主成分分析や、探索的因子分析が実行されます。因子分析を参照してください。
 変数のクラスタリング
変数のクラスタリング
([横長データ]または次元数を指定するアルゴリズムでは使用できません。)変数に対するクラスター分析を実行し、変数を重なりのないクラスターに分割します。似ているどうしの変数が同じクラスターに、また、似ていないどうしの変数が異なるクラスターに所属するように、分類します。同じクラスターに属する変数は、1つの主成分または1つの変数でよく表されます。求められた主成分は、該当のクラスター内のすべての変数の線形結合です。また、各クラスター内で最も代表的とみなされる変数も求められます。変数のクラスタリングを参照してください。
メモ: [変数のクラスタリング]は、[共分散行列から]または[非尺度化・非中心化]オプションを選択した場合でも、すべての計算に相関係数行列が使用されます。
モデルに基づく多変量管理図
指定した個数の主成分の計算式を保存し、「モデルに基づく多変量管理図」起動ウィンドウを開きます。起動ウィンドウでは、主成分の計算式が工程列に割り当てられています。このウィンドウで、工程列の追加や削除、時点IDの追加、履歴データの最終行の指定を行えます。これらの設定を行ってから、[OK]をクリックしてください。『品質と工程』のモデルに基づく多変量管理図を参照してください。
予測値のプロファイル
「プロファイル」起動ウィンドウを開きます。このウィンドウには、各変数の予測式が表示されます。各変数の予測式では、プロファイルの起動前に指定した個数の主成分が使用されます。必要に応じて誤差因子や別の予測式を追加してから、[OK]をクリックします。『プロファイル機能』のプロファイルを参照してください。
列の保存
保存のサブメニューが表示されます。
主成分の保存
指定された次元までの主成分スコアを計算する計算式を、データテーブルに保存します。この計算式で計算される主成分スコアは、欠測値のある行に対しては欠測値になります。
主成分スコアの計算式は、どの行列を分析対象にしたかによって異なります。
– [相関係数行列から]オプションを選んだ場合、i番目の主成分スコアは、i番目の固有ベクトルを係数にして求められた、中心化かつ尺度化されたデータの線形結合です。
– [共分散行列から]オプションを選んだ場合、i番目の主成分は、i番目の固有ベクトルを係数にして求められた、中心化されたデータの線形結合です。
– [非尺度化・非中心化]オプションを選んだ場合、i番目の主成分は、i番目の固有ベクトルを係数にして求められた、生データの線形結合です。
メモ: 指定した次元が相関係数行列のランクを超えている場合、保存される主成分の個数は相関係数行列のランクに設定されます。
データ値として主成分を保存
指定された次元までの主成分を、データテーブルに保存します。これらの列には、計算式ではなく、主成分スコアそのものが保存されます。
ヒント: このオプションは、横長データに使用してください。
低ランク近似の主成分を保存
(起動ウィンドウで、横長データまたは縦長データに対する推定方法として[ロバストPCA]を指定した場合のみ使用可能。)外れ値に対してロバストな低ランク近似行列の主成分スコアを保存します。
予測値の保存
指定した次元までの主成分から計算される予測値を、データテーブルの新しい列に保存します。
主成分の計算式として予測値を保存
予測値を、指定した個数の主成分の線形結合式として保存します。この計算式で使用された主成分もデータテーブルに保存されます。
Xモデルまでの正規化した距離を保存
各データ行から、指定した次元の主成分から計算される主成分モデルまでの距離(DModX)を、データテーブルの新しい列に保存します。DModXの値が大きいデータ行は、指定された次元までの主成分モデルでは十分に説明されず、その主成分モデルからは外れ値となっている可能性があります。『品質と工程』の監視の統計量の統計的詳細を参照してください。
データ行の余弦2乗を保存
指定した次元までの主成分から計算されるデータ行の余弦2乗を、データテーブルの新しい列に保存します。
データ行の偏寄与率を保存
指定した次元までの主成分から計算されるデータ行の偏寄与率を、データテーブルの新しい列に保存します。
回転後の成分を保存
([横長データ]または次元数を指定するアルゴリズムでは使用できません。)回転した後の主成分スコア(もしくは因子スコア)の計算式がデータテーブルに保存されます。このオプションは、[因子分析]オプションを使用した場合にのみ表示されます。この計算式で計算されるスコアは、欠測値のあるデータに対しては欠測値になります。
補完して主成分を保存
([横長データ]または次元数を指定するアルゴリズムでは使用できません。)欠測値を補完した後に算出した主成分スコアがデータテーブルに保存されます。列には、欠測値を補完したデータから主成分スコアを算出する計算式が保存されます。このオプションは、欠測値がある場合にのみ使用できます。
補完して回転後の成分を保存
([横長データ]または次元数を指定するアルゴリズムでは使用できません。)欠測値を補完した後に算出した回転後のスコアがデータテーブルに保存されます。列には、欠測値を補完したデータから回転後のスコアを算出する計算式が保存されます。このオプションは、欠測値があるデータに対して[因子分析]オプションを使用した場合にのみ表示されます。
欠測データ補完の計算式を保存
(データテーブルに欠測値がある場合のみ使用できます。)欠測値を含む列に関して、欠測値の推定に使用した計算式を、データテーブル内の新しい列に保存します。新しい列には、「補完された_<列名>」という名前がつきます。
 成分計算式の発行
成分計算式の発行
指定した次元までの主成分スコアの計算式を作成し、それを「計算式デポ」レポート内の計算式列スクリプトとして保存します。「計算式デポ」レポートが開いていない場合は、このオプションによって「計算式デポ」レポートが作成されます。『予測モデルおよび発展的なモデル』の計算式デポを参照してください。
 Xモデルまでの正規化した距離の計算式の発行
Xモデルまでの正規化した距離の計算式の発行
「計算式デポ」プラットフォームの数式列スクリプトとして、指定された次元までの正規化したDmodX(データから主成分モデルまでの距離)の計算式を保存します。「計算式デポ」レポートが開いていない場合は、このオプションによって「計算式デポ」レポートが作成されます。『予測モデルおよび発展的なモデル』の計算式デポを参照してください。
以下のオプションの詳細については、『JMPの使用法』の「JMPレポートのローカルデータフィルタ」、「JMPレポートの[やり直し]メニュー」、および「JMPレポートの[スクリプトの保存]メニュー」を参照してください。
ローカルデータフィルタ
データをフィルタリングするためのローカルデータフィルタの表示/非表示を切り替えます。
やり直し
分析を繰り返したり、やり直したりするオプションを含みます。また、[自動再計算]オプションに対応しているプラットフォームにおいては、[自動再計算]オプションを選択すると、データテーブルに加えた変更が、該当するレポートに即座に反映されるようになります。
プラットフォーム環境設定
現在のプラットフォームの環境設定を表示したり、現在のJMPレポートの設定に合わせて環境設定を変更したりできます。
スクリプトの保存
レポートを再現するためのスクリプトを保存するオプションが、保存先ごとに用意されています。
Byグループのスクリプトを保存
By変数の全水準に対するレポートを再現するスクリプトを保存するオプションが、保存先ごとに用意されています。起動ウィンドウでBy変数を指定した場合のみ使用可能です。