因子のシミュレーション設定
デフォルトでは、プロファイルの予測式で使われている因子(入力)が、シミュレータでも因子とみなされます。確率分布の位置やばらつきを変更するオプションがあり、それにより因子の乱数で用いる確率分布を変更できます。
固定
すべてのシミュレーションにおいてプロファイルの現在値に因子を固定します。
ランダム
指定された確率分布に基づき、因子に対して乱数を生成します。[ランダム]を選択すると、確率分布に関するオプションが表示されます。オプションの詳細については、連続尺度の因子とカテゴリカルな因子を参照してください。
メモ: デフォルトの確率分布は、現在の因子設定を母平均とし、また因子の範囲を5で割ったものを母標準偏差とする正規分布です。配合因子が含まれる場合、標準偏差は配合限界値の範囲を5で割って求められます。プロファイルの因子設定を変更すると、正規分布の平均は自動的に更新されます。正規分布以外の確率分布でも、因子設定を変更するとパラメータが自動的に更新されます。三角分布では3つのパラメータがすべて更新され、Cauchy分布では最頻値(モード)が更新され、Johnson Su分布では、qが更新されます。
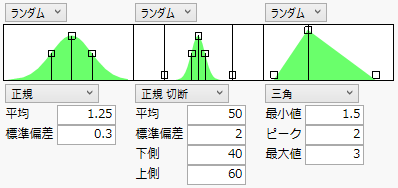
図8.5 3つの確率分布の例
式
JSL(JMPスクリプト言語)の式に基づいて因子の値を生成します。これにより、分析者独自の確率分布も指定できます。たとえば、負の値が生じないような切断正規分布の乱数を生成するには、以下のような式にします。
Max(0,RandomNormal(5,2))式を入力した後、[リセット]ボタンをクリックすると式が設定されます。
多変量
多変量正規分布に基づく乱数を生成します。まず、各因子に対しては、平均と標準偏差を指定してください。また、それらに加えて、相関行列を「X相関の指定」レポートに指定してください。因子間に相関があると考えられる場面で、このオプションを利用することが考えられます。
図8.6 [多変量]オプションで相関行列を定義する
ヒント: すべての因子に同じ設定を指定するには、Ctrlキーを押しながら、希望する設定を選択します。
連続尺度の因子
連続尺度の因子の場合、利用可能な確率分布は、『JMPの使用法』の乱数関数に説明されている標準的な確率分布です。ただし、以下のような確率分布も、シミュレータでは利用できます。
正規 加重
与えられた平均と標準偏差を持つ正規分布から乱数を生成しますが、このとき重みを与えます。[正規 加重]オプションは、正規分布の裾に位置する非常に稀なイベントをシミュレートするための特殊な方法です。不適合率が非常に低いような状況をシミュレートするときに役立ちます。シミュレータの統計的詳細を参照してください。
正規 切断
下限と上限をもつ切断正規分布から乱数を生成します。生成された乱数のうち、下限や上限を超える値は廃棄され、残ったものだけが採択されます。品質検査において、該当の因子に関する特性が仕様限界を満たさないと廃棄しているような状況をシミュレートするのに役立ちます。
正規 打ち切り
下限と上限をもつ切断正規分布から乱数を生成します。生成された乱数のうち、限界を超えているものがその限界値に置き換えられます。このため、限界値において点の密度が高くなります。入力が仕様限界を満たさない場合に仕様限界内に収まるまでやり直しをするような状況をシミュレートするのに役立ちます。
標本
データテーブル内の因子の列からランダムに値を選択することにより乱数を生成します。
外部
他のデータテーブル内の列からランダムに値を選択することにより乱数を生成します。このオプションを選択した場合、用いるデータテーブルと列を選択してください。
ヒント: すべての分布に同じ設定を指定するには、Ctrlキーを押しながら、希望する分布を選択します。
メモ: [標本]または[外部]を選択すると、[連携]チェックボックスが表示されます。このチェックボックスは、2つ以上の因子が[標本]または[外部]に設定される場合に使用されます。チェックマークをつけると、それらの因子の値はデータテーブル内の同じ行からランダムに抽出されます。この機能により、連携された2つの列のあいだの相関構造を再現できます。[連携]オプションを、異なるデータテーブルに属する2つの列に使用したいときは、各列の行数が等しいことを確認してください。
カテゴリカルな因子
カテゴリカルな因子の場合、各カテゴリに指定された確率をパラメータとする多項分布から乱数が生成されます。デフォルトでは、その確率はデータテーブルにおいて観測された割合に設定されています。プロット内でハンドルを使用するか、「確率」列で数値を変更することでその確率を変更することができます。確率の合計は1になります。
メモ: 選択した確率の合計が1にならない場合、[シミュレート]ボタンをクリックすると合計が1になるよう自動的に補正されます。
因子のシミュレーションが[ランダム]に設定されると、因子がカテゴリカルな場合は確率関数(確率質量関数)のグラフが、因子が連続尺度の場合は確率密度関数のグラフが表示されます。グラフは連続分布の場合、確率分布の形状を描いています。グラフ上に点(ハンドル)が表示されており、この点をドラッグすると分布が変化します。正規分布の場合、平均と、平均±1標準偏差に点が配置されています。切断正規分布と打ち切り正規分布では、上下限値にも点があります。一様分布では上下限値に、三角分布では上下限値と最頻値(モード)に点が配置されています。
配合因子
配合因子の場合、2つの確率分布が利用可能です。配合因子は、同じ種類の確率分布から生成される必要があります。ただし、固定の配合因子とランダムな配合因子を組み合わせることはできます。
一様配合
単体上や凸多面体上に一様乱数の点を生成します。各因子に対して、下限と上限を指定することもできます。生成された乱数は、混合制約を満たしています。このオプションによる乱数生成では、多面体上の一様乱数を生成するJSL関数であるPolytope Uniform Random 関数が裏で使用されます。『スクリプト構文リファレンス』のユーティリティ関数を参照してください。
Dirichlet配合
因子ごとにパラメータaをもつDirichlet分布から乱数を生成します。Dirichlet分布の確率密度関数は次のように計算されます。
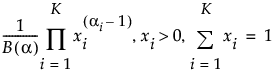
ここで、B(a)は多変量ベータ関数で、正規化定数です。[Dirichlet配合]オプションは、因子の境界が、単体である配合領域である場合(つまり、「三角形」全体を領域にする場合)にしか使えません。
![[多変量]オプションで相関行列を定義する [多変量]オプションで相関行列を定義する](../jmp/images/2-101.png)