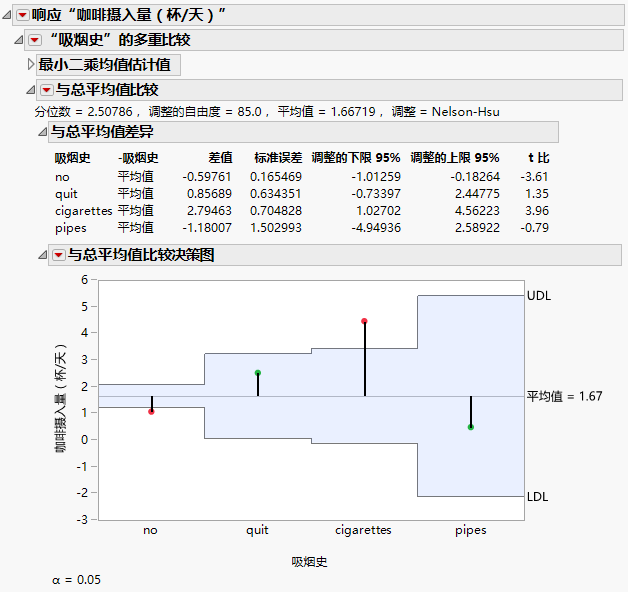
与总平均值比较
选择“多重比较”选项时,您可以选择要与总体平均值进行的初始比较。该选项将指定水平的均值与这些水平的总均值进行比较。它显示一个表(其中显示总均值差值的置信区间)和一个图(其中显示决策限)。比较所用的方法称为均值分析(ANOM) (Nelson et al. 2005)。ANOM 是一种多重比较过程,用来控制针对总均值的所有配对比较的联合误差率。有关基于 Lipid Data.jmp 样本数据表的报表,请参见图 3.55。
ANOM 的显示可能与方差分析类似。不过,根本上的不同在于:ANOM 标识其均值与所有水平的总均值存在差异的水平。相反,方差分析检验均值自身的差值。
在“与总平均值比较”报表的顶部,您会发现:
Quantile
用于构造决策限的 Nelson h 统计量的值。
调整的自由度
用于构造决策限的自由度。
平均值
平均均值。对于最小二乘估计值,平均均值是组最小二乘均值的加权平均值。该加权平均值表示中性设置(用于计算组最小二乘均值)下的总均值。
具体而言,平均最小二乘均值是权重与矩阵 L(X′X)-1L′ 的对角线元素成反比的加权平均值。其中,L 是用于计算组最小二乘均值的系数所构成的矩阵。有关最小二乘均值的技术定义,请参见 SAS Institute Inc.(2020b)。
对于用户定义的估计值,平均均值也按类似方式定义。不过,在这种情况下 L 是用于定义估计值的系数所构成的矩阵。
调整
说明用于获取临界值的方法:
Nelson
提供精确临界值和 p 值。尽可能使用,特别是在估计值不相关时。
Nelson-Hsu
基于使用 Hsu 因子分析近似 (Hsu 1992) 提供近似临界值和 p 值。在无法获取精确值时使用。
Sidak
在 Nelson 和 Nelson-Hsu 均失败时使用。
有关技术细节,请参见 SAS Institute Inc.(2020b)。
“与总平均值比较”报表菜单提供三个选项:
与总平均值差异
对于组均值与总均值的每次比较,该报表提供以下详细信息:
• 要比较的水平
• 差值 — 估计的差值
• 标准误差 — 差值的标准误差
• 置信区间的上下限
• t 比 - “差值”与“标准误差”列之比
与总平均值比较决策图
该决策图在每个组的均值处标绘一个点。在平均均值处标绘了一条水平线。同时标绘上决策限和下决策限。假定与组均值对应的点落在这些限值之外。这表示基于指定显著性水平下的均值分析检验,组均值与总均值存在差异。显著性水平显示在图的下方。
“与总平均值比较决策图”报表菜单包含以下选项:
显示汇总报表
生成显示每组的估计值、决策限和超出限值的表
显示选项
提供用于控制图显示的若干选项。
计算调整的 p 值
将包含 p 值(概率>|t|)的列添加到“与总平均值比较”报表。请注意,计算不平衡设计的精确临界值和 p 值要求复积分,计算起来可能较为困难。针对此类分位数的计算若失败,则计算 Sidak 分位数,但不提供 p 值。
“与总平均值比较”的示例
考虑 Lipid Data.jmp 样本数据表。您关注在控制饮酒状况和心脏病史的前提下四种吸烟史类别中是否有任何类别的咖啡摄入量(杯/天)均值与咖啡摄入量的总平均值有明显不同。您指定包含咖啡摄入量(杯/天)的模型作为响应,将吸烟史、饮酒状况和心脏病史作为模型效应。
1. 选择帮助 > 样本数据文件夹,然后打开 Lipid Data.jmp。
2. 选择分析 > 拟合模型。
3. 选择咖啡摄入量(杯/天)并点击 Y。
4. 选择吸烟史、饮酒状况和心脏病史,然后点击添加。
5. 点击运行。
6. 点击“响应‘咖啡摄入量(杯/天)’”旁边的红色小三角并选择估计值 > 多重比较。
7. 从“选择效应”列表中,选择吸烟史。
8. 在“选择初始比较”列表中,选择与总平均值比较 - ANOM。
9. 点击确定。
结果显示在图 3.55 中,它说明在咖啡摄入量方面非吸烟者和吸烟者的最小二乘均值与总平均值有显著不同。
图 3.55 与“分级”的总平均值比较