反復測定の例
「モデルのあてはめ」プラットフォームで反復測定混合モデルをあてはめて、2つの新薬のいずれかにコレステロール値を下げる効果があるかどうかと、処置と時刻の間に交互作用があるかどうかを調べましょう。コレステロールを下げるための2剤の実薬を、プラセボ群やコントロール群（対照群）と比較する試験が行われました。コレステロール値が高い20名の患者に対し、4種類の処置（2種類の実薬群、コントロール群、プラシボ群）のいずれかが無作為に割り付けられました。各患者の総コレステロール値が、4、5、6月の第1日目において、午前・午後で測定されました（計6回の測定）。
背景
このような反復測定データの統計分析には、2つの古典的なアプローチがあります。
• 多変量分散分析（MANOVA）
• 分割実験データとみなして、一変量の分散分析（ANOVA）の枠組みで分析する方法。Huynh‐Feldt（1976）の修正や、Greenhouse‐Geisser（1959）の修正が適用されることもある。
これらの2つの方法は、JMPでは「モデルのあてはめ」の［MANOVA］手法でも実行できます。これら2つの統計手法は、異なった誤差共分散構造を想定しています。多変量分散分析の枠組みでは、共分散構造として無構造（unstructured）を仮定しています。一方、分割実験データの一変量分散分析の枠組みでは、各患者の変量効果に、独立で同一な誤差が加わることにより、応答の共分散構造が決まると想定しています。変量効果と誤差が独立である場合、この枠組みの応答の共分散構造は、反復測定モデルの誤差に複合対称（compound symmetry）の共分散構造を仮定したものと同じになります。
これら2つのモデル（誤差の共分散構造を無構造としたモデルと、複合対称としたモデル）では、処置に対する検定において、検定結果が大きく異なる場合があります。両モデルにおいて共分散パラメータはデータから推定されます。無構造を仮定した場合、推定する共分散パラメータが多すぎる状態になっているかもしれません。反復測定データを分析するときには、ほどよい共分散構造をモデルで用いる必要があります。
• 共分散構造のパラメータが過度に多いと、あまり複雑でない共分散構造を仮定した場合よりも、処置の差を検出する検出力が小さくなります。
• 仮定した共分散構造が過度に単純で、真の共分散構造を含んでいないと、第1種の誤りの確率が保たれなくなります。つまり、共分散構造を過度に単純にしてしまうと、実質的な有意水準が、名目的な有意水準を超えてしまう可能性があります。また、逆に、標準誤差が大きくなって、実質的な有意水準が減少してしまう場合もあります。
共分散構造
［混合モデル］手法には、さまざまな共分散構造が用意されています。反復測定データは、Toeplitz分散構造や1次自己相関（AR(1)）の共分散構造に従っている場合がよくあります。これらの構造は、多くの反復測定データの特徴をよく捉えていると同時に、推定するパラメータ数が少なくて済みます。AR(1)構造やToeplitz構造は、各時点での分散が同じであると仮定します。一方、異分散Toeplitz構造は、時点ごとに異なる分散を仮定します。反復共分散構造の要件を参照してください。
この例では、4つの共分散構造をあてはめます。観察時点数は6時点です（J=6は）。
• 共分散構造: 無構造。［無構造］のモデルは、合計でJ(J+1)/2個の共分散パラメータをすべてあてはめます。この例では、21個の共分散パラメータがあります。
• 共分散構造: 残差。［残差］モデルは、単なる、独立で同一な誤差です。この例では、患者の効果を変量効果として含めます。よって、共分散パラメータは全部で2個です。
• 共分散構造: Toeplitz。異分散Toeplitz構造には、2J‐1個の共分散パラメータがあります。この例では、11個の共分散パラメータがあります。
• 共分散構造: AR(1)。このモデルには、2つの共分散パラメータがあります。1つのパラメータは分散です。もう1つのパラメータは、時間の経過に伴う共分散の変化を表します。
モデルの適合度は、AICcで評価します。他にも、BICによって、モデルを比較することもできます。この例では、AICcとBICのいずれの規準を用いても、同じモデルが選択されます。最良の共分散構造を選択し、分析を続けます。
ヒント: 指定方法の違いを確認するために、「モデルのあてはめ」起動ウィンドウを開いたままにしておいてください。
データの構造
「Cholesterol.jmp」データテーブルは、反復測定データの記録によく使用される形式を取っています。［混合モデル］手法を使ってこのデータを分析するには、「Cholesterol Stacked.jmp」のようにコレステロールの測定値が1つずつ個別の行に入っていなければなりません。「Cholesterol.jmp」の形式から「Cholesterol Stacked.jmp」のようなデータを作成するため、［テーブル］>［列の積み重ね］を用いました。
積み重ねたデータテーブルの「日数」列では、実験の開始日から測定日までの経過日数が、計算式によって算出されています。この列は連続尺度になっています。共分散構造としてAR(1)を使う場合、時点を表す列は連続尺度でなければなりません。
共分散構造: 無構造
最初に、共分散構造が無構造であるモデルをあてはめましょう。
1. ［ヘルプ］>［サンプルデータフォルダ］を選択し、「Cholesterol Stacked.jmp」を開きます。
2. ［分析］>［モデルのあてはめ］を選択します。
3. ［ダイアログを開いたままにする］にチェックを入れ、次の例に移る際に起動ウィンドウに戻れるようにしておきます。
4. 「Y」を選択し、［Y］をクリックします。
5. 「手法」リストから［混合モデル］を選択します。
6. 「処置」、「月」、「午前/午後」を選択し、［マクロ］>［完全実施要因］を選択します。
図8.12 「モデルのあてはめ」起動ウィンドウの［固定効果］タブでの指定
7. ［反復構造］タブを選択します。
8. 「構造」リストから、［無構造］を選択します。
9. 「時刻」を選択し、［反復］をクリックします。「反復」列が被験者内の反復測定値を定義します。
10. 「患者」を選択して［個体］をクリックします。
メモ: ［無構造］の共分散モデルでは、各個体（各被験者）は、一意なIDで識別されていなければいけません。この例では、患者は処置から枝分かれしています。このとき、患者のIDが、全体ではなく、処置ごとの通し番号になっていたとします。そのような場合、［無構造］で分析を実行しようとすると、警告が表示されます。各患者が全体で一意に識別されるように、IDを振り直す必要があります。計算式で、処置の値とIDの値を組み合わせることにより、一意なIDの列を作成しても構いません。
図8.13 「モデルのあてはめ」起動ウィンドウの［反復構造］タブでの指定
11. ［実行］をクリックします。
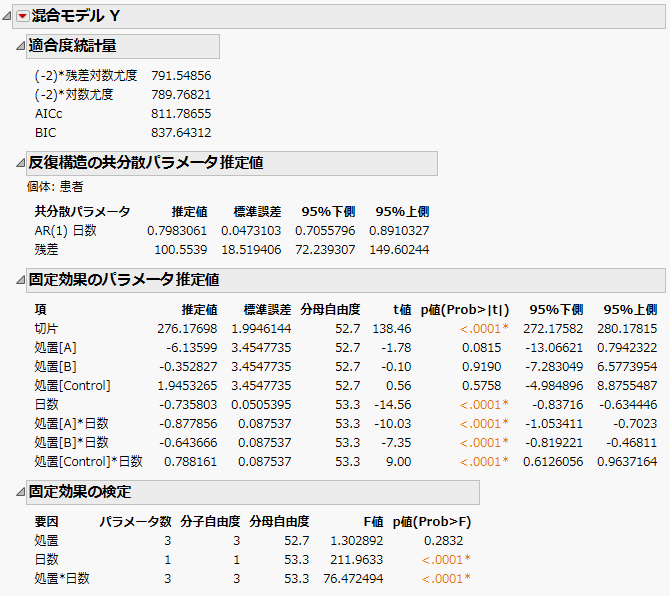
Figure 8.14のような「混合モデル」レポートが表示されます。3つのモデルをAICcまたはBICを使って比較したいので、「適合度統計量」レポートを見てみましょう。無構造モデルのAICcは703.84です。
「反復構造の共分散パラメータ推定値」レポートには、全部で21個の共分散パラメータ推定値が表示されています。予想されるように、近い時点間での共分散は、遠い時点間での共分散よりも大きくなっています。また、分散は時間の経過とともに大きくなっているようです。
図8.14 無構造の共分散構造の「混合モデル」レポート
共分散構造: 残差
分割実験モデルをあてはめる際は、患者の列を変量効果に指定し、共分散構造に［残差］を指定します。
1. 共分散構造: 無構造のstep 1からstep 7までを行います。
2. ［反復構造］タブの「構造」リストから［残差］を選択します。
3. 前回の例の続きで行う場合は、「時刻」と「患者」を削除してください。
削除しなかった場合は、「共分散構造として「残差」が選択されているので、［反復］や［個体］に指定された列を無視して分析を行います。」という警告が表示されるので、そこで［OK］をクリックして分析を続行してください。
4. ［変量効果］タブをクリックします。
5. 「患者」を選択し、［追加］をクリックします。
6. 「変量効果」タブのリストボックスで「患者」を選択し、次に「列の選択」のリストボックスで「処置」を選択してから、［枝分かれ］をクリックします。
図8.15 「モデルのあてはめ」起動ウィンドウの［変量効果］タブでの指定
7. ［実行］をクリックします。
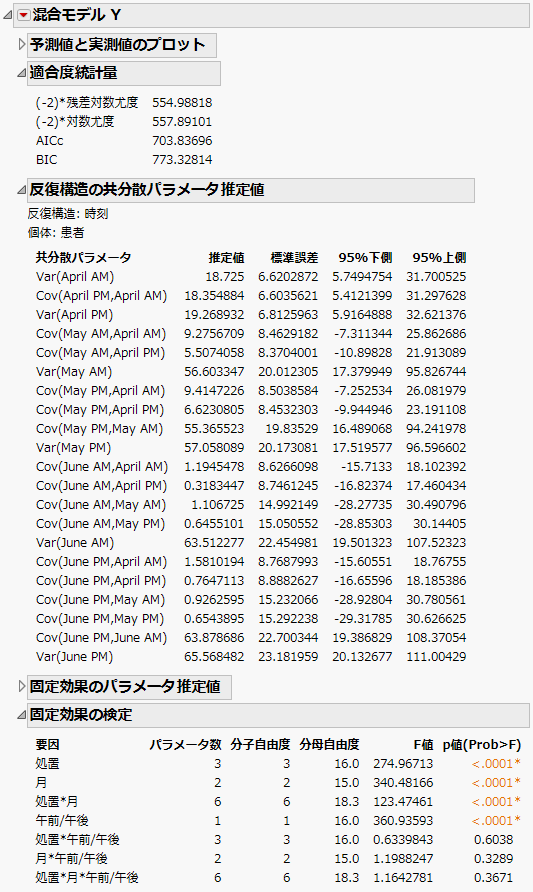
Figure 8.16のような「混合モデル」レポートが表示されます。「適合度統計量」レポートでAICcを見ると、無構造モデルでは703.84だったのに対して、分割実験モデルでは832.55となっています。
分割実験モデルにおける2つの分散パラメータの推定値は、「変量効果の共分散パラメータ推定値」レポートに表示されます。これらの推定値は、「患者」の分散と残差誤差の分散を推定した値です。
図8.16 分割実験モデルの「混合モデル」レポート
共分散構造: Toeplitz
［Toeplitz 異分散］構造を使ってモデルをあてはめます。
1. 共分散構造: 無構造のstep 1からstep 6までを行います。
2. 前回の例の続きで行う場合は、［変量効果］タブの「患者[処置]」を選択して「削除」をクリックします。
反復測定モデルでは、変量効果と反復効果の両方は推定できなかったり、両方を推定するにはデータが少なすぎることは良くあります。
3. ［反復構造］タブを選択します。
4. 「構造」リストで［Toeplitz 異分散］を選択します。
5. 「時刻」を選択し、［反復］をクリックします。
6. 「患者」を選択して［個体］をクリックします。
図8.17 「モデルのあてはめ」起動ウィンドウの［反復構造］タブでの指定
7. ［実行］をクリックします。
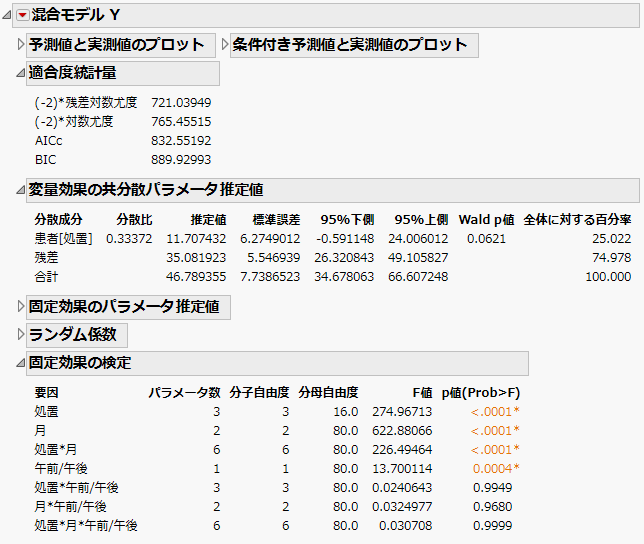
図8.18 Toeplitz異分散構造の「混合モデル」レポート
メモ: JMPの［混合モデル］手法は相関、SASのPROC MIXEDは共分散をレポートします。
「適合度統計量」レポートを見ると、「Toeplitz 異分散構造」モデルのAICcは788.03です。この数値を、「残差」モデルの832.55と「無構造」モデルの703.84と比べてみましょう。
「Toeplitz 異分散」構造では、11個の共分散パラメータの推定値を計算しなければなりません。これらの推定値は、「反復効果の共分散パラメータ推定値」レポートに表示されます。Toeplitz相関の推定値に続き、各時点の分散推定値が表示されます。この行列がどのようにパラメータ化されるかについては、反復測定の統計的詳細を参照してください。
共分散構造: AR(1)
最後に、共分散構造がAR(1)構造であるモデルをあてはめます。
1. 共分散構造: 無構造のstep 1からstep 6までを行います。
2. 前の例から続けて分析を行う場合は、「反復」ボックスで「時刻」を選択し、［削除］をクリックします。
AR(1)では、「反復」する値が連続尺度の変数でなければなりません。
3. 「構造」リストから、［AR(1)］を選択します。
4. 「日数」を選択し、［反復］をクリックします。
図8.19 「モデルのあてはめ」起動ウィンドウの［反復構造］タブでの指定
5. ［実行］をクリックします。
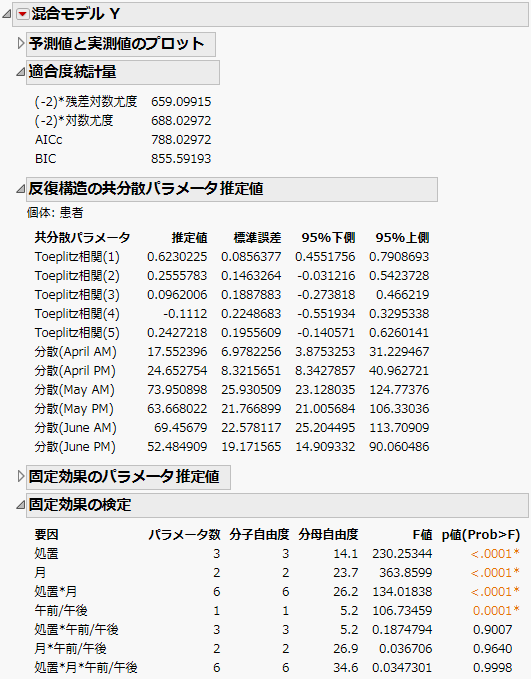
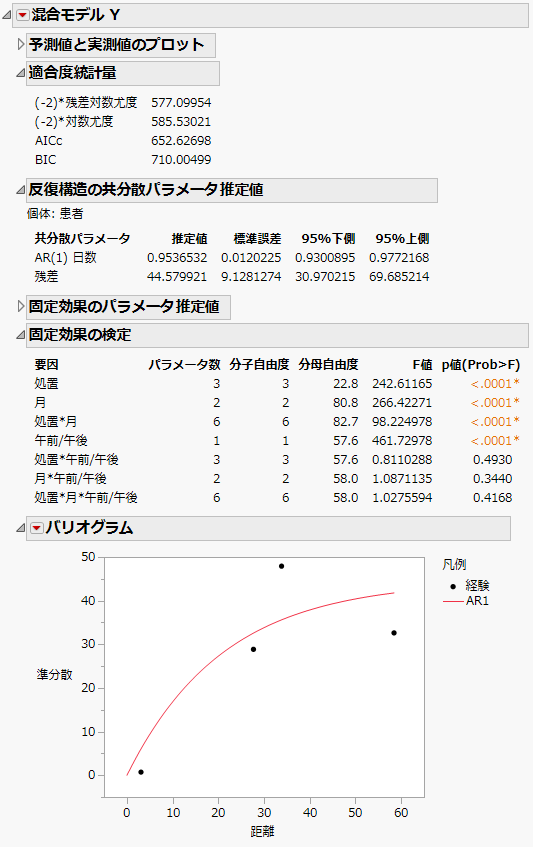
Figure 8.20のような「混合モデル」レポートが表示されます。「適合度統計量」レポートを見ると、「AR(1)」モデルのAICcは652.63です。この数値を、「残差」モデルの832.55と「無構造」モデルの703.84、「Toeplitz 異分散」モデルの788.03と比較しましょう。AICc規準に基づくと、4つのモデルのうち「AR(1)」モデルが最良と言えます。
AR(1)構造には、2つの共分散パラメータがあります。これらの推定値は、「反復効果の共分散パラメータ推定値」レポートに表示されます。「AR(1)日数」に表示されている推定値は、AR(1)構造での相関を決めるrの推定値になっています。
バリオグラムには、経験的準分散とAR(1)モデルの曲線が表示されます。「日数」に、ゼロでない値が5つしかないため、距離が4つしか測定できず、点も4つしか表示されません。AR(1)構造は、適切だと考えられます。他の構造について調べるには、「バリオグラム」の赤い三角ボタンのメニューからオプションを選択します。「バリオグラム」のオプションの詳細については、バリオグラムを参照してください。
図8.20 AR(1)の共分散構造の「混合モデル」レポート
AR(1)構造を使ったさらなる分析
AR(1)モデルの適合度が最も優れているため、これをモデルに採用し、分析を進めます。「固定効果の検定」レポートには、「処置」と「月」の交互作用と「午前/午後」の主効果が有意であることが示されています。ここでは、これらの有意な効果について調べます。
1. 「混合モデル」の赤い三角ボタンをクリックし、［周辺予測値プロット］>［プロファイル］を選択します。
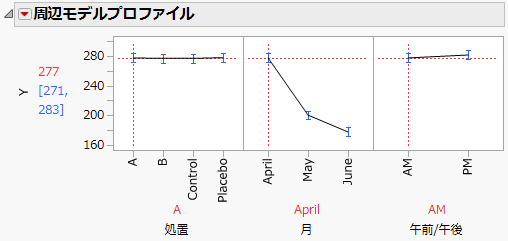
「周辺モデルプロファイル」レポート（Figure 8.21）では、「処置」、「月」、「午前/午後」をさまざまに設定した場合のコレステロール（Y）への効果が確認できます。
2. 「月」のプロットで、赤い縦の点線を「April」から「May」へ、次に「June」へとドラッグしてみましょう。
「AM」におけるYの平均予測値は、「April」の277.4から「June」の177.7へと下がります。
3. 「処置」のプロットで、赤い縦の点線を「A」から「B」へドラッグします。
「月」のプロットで点線を「April」から「June」へとドラッグすると、処置が「B」の場合の「AM」におけるYの平均予測値が「April」の277から「June」の191へと下がることがわかります。
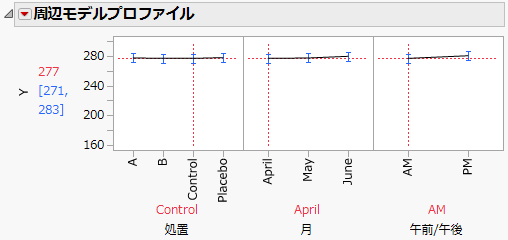
4. 「処置」のプロットで、縦の点線を「Control」（コントロール）へ、そして「Placebo」（プラセボ）へドラッグします。
「処置」が「Control」や「Placebo」の場合には、時間が経っても、コレステロールは減少しません（Figure 8.22）。
次に、「午前/午後」の効果を調べます。
5. 赤い縦線をドラッグすることで、「処置」と「月」のすべての水準の組み合わせにおける午前と午後の違いを見てください。
12個の組み合わせすべてで、午前より午後の方がコレステロールが高くなっているので、「午前/午後」の主効果の存在が示唆されます。
5月においては、処置「A」の方が、処置「B」よりもコレステロールが低くなっているようです。もしこの差が統計的に有意であるなら、5月においては、処置「A」の平均は、処置「B」の平均よりも小さいことを意味しています。次節の6月におけるすべての処置の比較では、6月における各処置の平均を比較しています。
図8.21 処置A群の周辺プロファイル
図8.22 コントロール群の周辺プロファイル
6月におけるすべての処置の比較
調査は、4～6月の3ヶ月にわたって行われました。ここでは、6月の午後の測定値に対し、処置が与える影響を調べます。
1. 「混合モデル」の赤い三角ボタンをクリックし、［多重比較］を選択します。
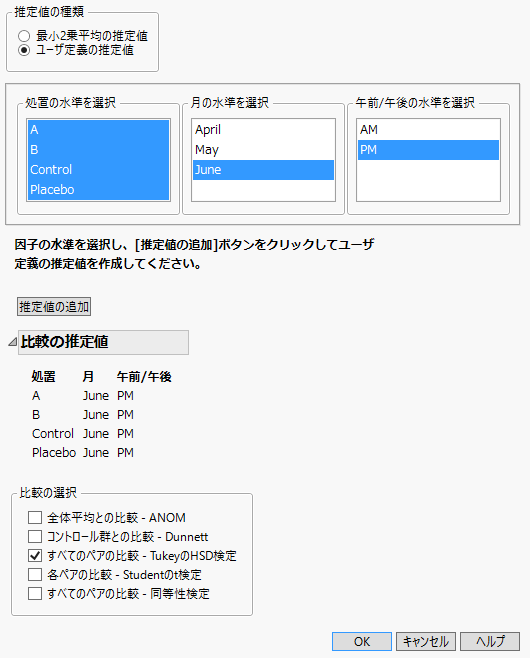
2. 「推定値の種類」リストから［ユーザ定義の推定値］を選択します。
3. 「処置の水準を選択」パネルで、4つの処置をすべて選択します。
4. 「月の水準を選択」パネルで、「June」を選択します。
5. 「午前/午後の水準を選択」パネルで、「PM」を選択します。
6. ［推定値の追加］をクリックします。
7. 「比較の選択」リストで、［すべてのペアの比較 - TukeyのHSD検定］を選択します。
図8.23 「多重比較」ウィンドウで設定を終えたところ
8. ［OK］をクリックします。
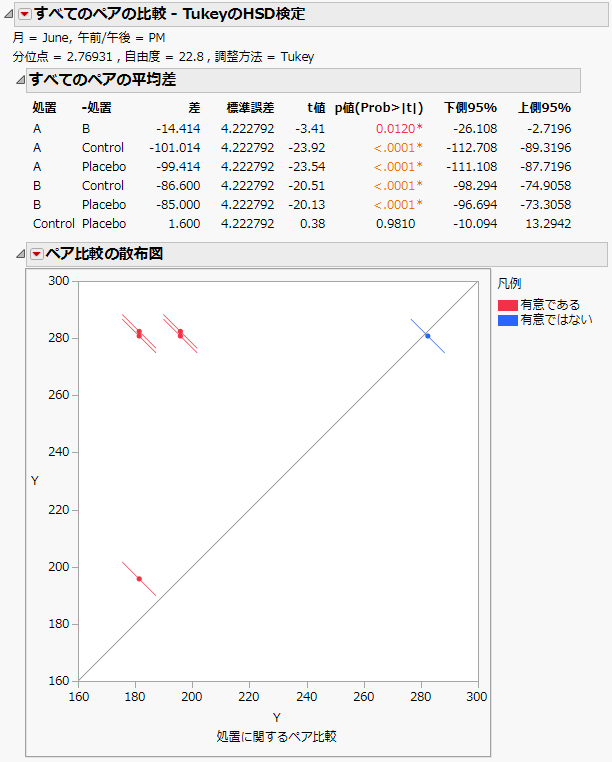
図8.24 6月の午後のすべての処置に対する「すべてのペアの比較 - TukeyのHSD検定」レポート
「すべてのペアの比較 - TukeyのHSD検定」レポートには、「すべてのペアの平均差」レポートと「ペア比較の散布図」が表示されます。「June」の「PM」においては、「Control」と「Placebo」を除くすべての処置が有意に異なっています。
処置「A」と「B」の差について検討してみましょう。平均の差は-14.414、信頼区間は-26.108～-2.7196です。6月午後では、処置「A」のコレステロール値は、処置「B」よりも、2.7～26.1低くなっていると結論できます。また、処置「A」と「B」は、どちらも「Control」および「Placebo」に比べて効果が大きいことがわかります。
AR(1)誤差構造の回帰モデルの例
前節までの例では、名義尺度の列である「月」と「午前/午後」を使って、4つの共分散構造を比較しました（なお、共分散構造に［無構造］を指定する場合には、時点の列が名義尺度になっていなければいけません）。そして、共分散構造としてAR(1)構造が良いと判断して、分析を進めました。
ここでは、連続尺度の列「日数」によって時点の効果を表すことにしましょう。時点の効果を連続尺度にすると、（その回帰モデルが正しければ）任意の時点におけるコレステロールを予測できるようになります。
1. 共分散構造: AR(1)のstep 1～step 4の手順を行い、「モデルのあてはめ」起動ウィンドウに戻ります。
2. ［固定効果］タブに指定されているすべての固定効果を選択し、［削除］をクリックします。
3. 「処置」と「日数」を選択し、［マクロ］>［完全実施要因］を選択します。
図8.25 「モデルのあてはめ」起動ウィンドウの［固定効果］タブ
4. 「モデルの指定」の赤い三角ボタンをクリックし、［多項式の中心化］の選択を解除します。
メモ: デフォルトの設定では、交互作用項で使用される連続変数は中心化されます。［多項式の中心化］オプションの選択を解除することによって、このような連続変数が中心化されないようにできます。
5. ［実行］をクリックします。
Figure 8.26のような「混合モデル」レポートが表示されます。「処置」と「日数」の交互作用が有意になっています。これは、日数を説明変数とした回帰直線の傾きが、薬剤によって異なることを示しています。
メモ: ある日数における予測値を求めるには、プロファイルを用いてください。『プロファイル機能』のプロファイルを参照してください。
図8.26 AR(1)共分散構造の連続時間モデルの「混合モデル」レポート
